CEMC Banner

Problem of the Week
Problem A
Wrapping Presents

When Jack wraps a box, he first does a test to determine if his sheet of wrapping paper is long enough.

To do this, Jack places his box on top of the wrapping paper so that one edge of the box is lined up with the width of the wrapping paper. He then flips the box along the length of the paper so that each of its four sides touches the paper once.

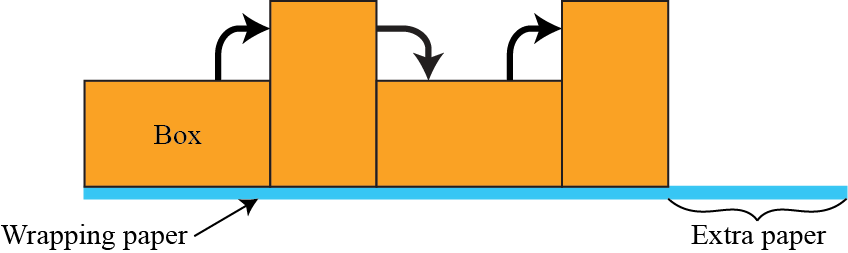
Four identical rectangles representing the different positions of the box during the test. The rectangles lie side by side on a horizontal line representing the wrapping paper. The line extends beyond the rectangles indicating extra paper. The first and third rectangles have their longer sides touching the paper and the second and fourth rectangles have their shorter sides touching the paper. Arrows indicate movement from the first rectangle to the second, from the second to the third, and from the third to the fourth.

If there is at least \(6\) cm of extra paper left after the last flip, Jack concludes that his sheet of wrapping paper is long enough. If there is less than \(6\) cm of extra paper left after the last flip, Jack rotates his box so a different edge of his box is lined up with the wrapping paper and tries his test again.

Jack wants to wrap a box with dimensions \(20\text{ cm} \times 12 \text{ cm}\times 8 \text{ cm}\).
He has a sheet of wrapping paper that is \(62\) cm long.

Would this sheet of wrapping paper be long enough to wrap his box? If so, how should he position his box on the wrapping paper at the beginning of his test? You can assume the wrapping paper is wide enough to wrap the box. Justify your answer.