CEMC Banner

Problem of the Week
Problem B and Solution
Piscine’s Pool Pavers

Problem

Piscine is replacing the paving stones around her inground pool. Her pool is \(10\) m by \(5\) m, and is surrounded by a \(1.5\) m border of paving stones.

  1. How many square metres of paving stones will she need in total?

  2. If each paving stone is \(25\) cm by \(40\) cm, in theory, how many paving stones will she need?

  3. Will your answer in part b) actually be enough? Try fitting the stones in the space to see whether Piscine can complete the border with exactly that number of stones, or whether there will be waste, requiring some extras.

    4. The rectangular pool and its border. The outer edge of the border is also rectangular.

    Solution

    1. The area of paving stones needed can be calculated in several ways. In the two methods shown below, we divide the area into four rectangles.
      Method 1: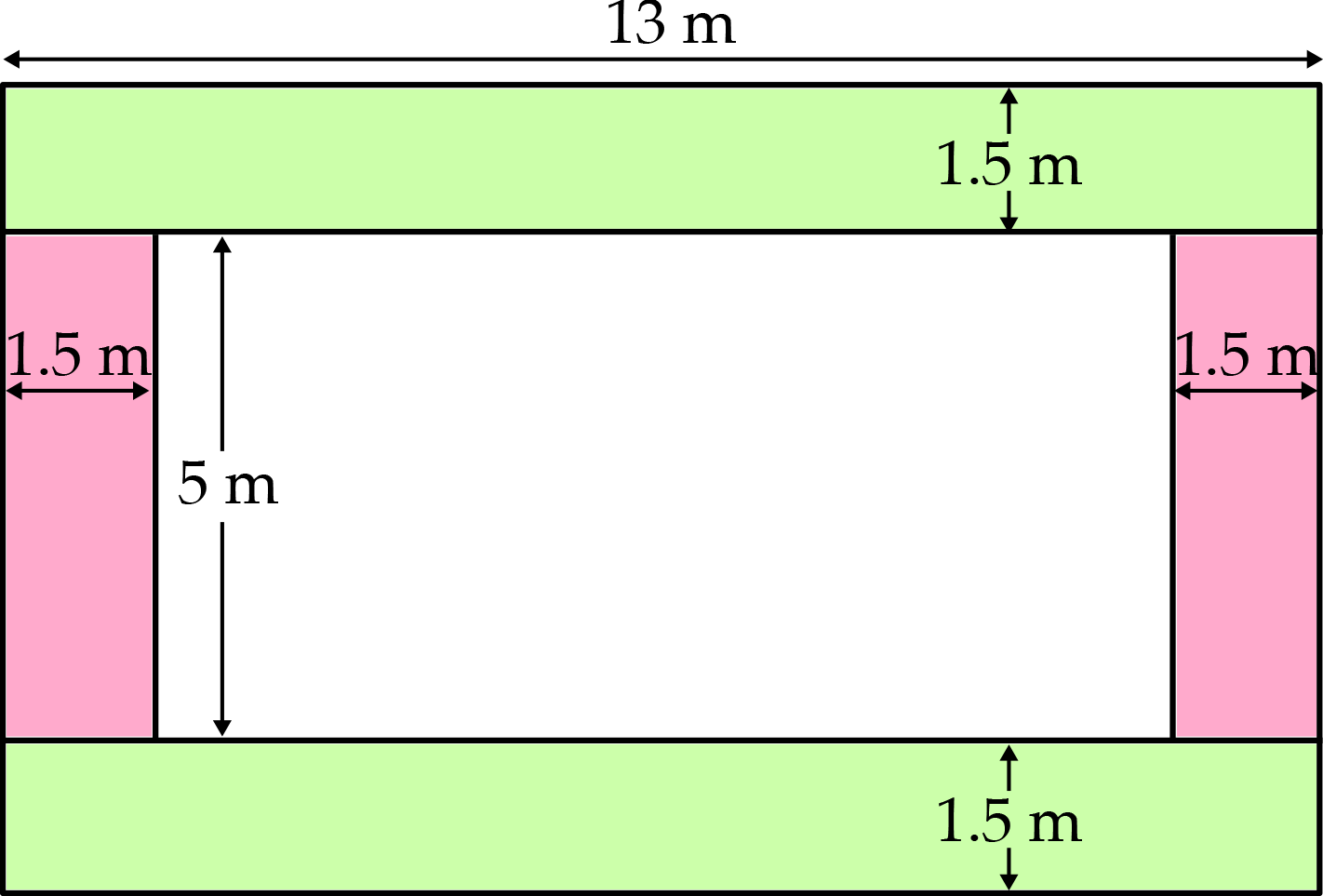

      Top and bottom rectangles with dimensions 13 metres by 1.5 metres are lined up 5 metres apart. Their longer sides are horizontal. Two side rectangles with dimensions 5 metres by 1.5 metres lie in between the top and bottom rectangles at either end. Their longer sides are vertical.

      Top and Bottom Areas:
      \((13 \times 1.5) \times 2 = 39\text{ m}^2\)

      Side Areas:
      \((5 \times 1.5) \times 2 = 15\text{ m}^2\)

      Total Area:
      \(39+15=54\text{ m}^2\)

      Method 2:

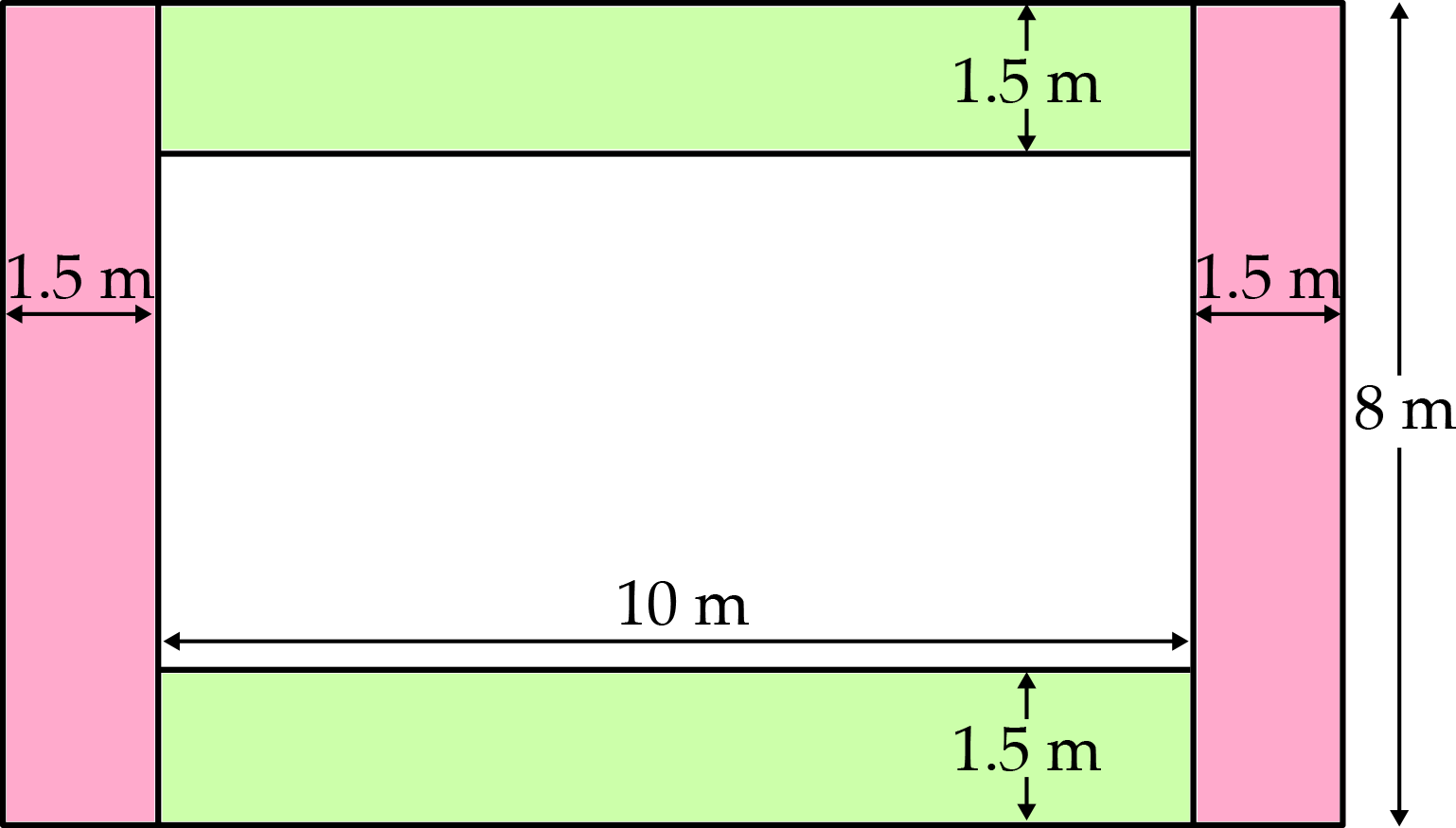
      Two side rectangles with dimensions 8 metres by 1.5 metres are lined up 10 metres apart. Their longer sides are vertical. Top and bottom rectangles with dimensions 10 metres by 1.5 metres lie in between the side rectangles at either end. Their longer sides are horizontal.

      Top and Bottom Areas:
      \((10 \times 1.5) \times 2 = 30\text{ m}^2\)

      Side Areas:
      \((8 \times 1.5) \times 2 = 24\text{ m}^2\)

      Total Area:
      \(30+24=54\text{ m}^2\)

      Either way, we see that Piscine needs 54 m\(^2\) of paving stones.

    2. First we need to calculate the area of each paving stone in \(\text{m}^2\). Since \(1 \text{ cm} = 0.01 \text{ m}\), each paving stone is 0.25 m by 0.4 m. So the area of each paving stone is \[0.25 \times 0.4 = 0.1 \text{ m}^2\] To calculate the number of paving stones needed, we can divide the total area we calculated in part a) by the area of each paving stone. Thus, the number of paving stones needed is \(54 \div 0.1 = 540\) tiles.

    3. If we divide the area as shown in Method 2 from part a), then the 540 paving stones will fit exactly in the space, as shown below.

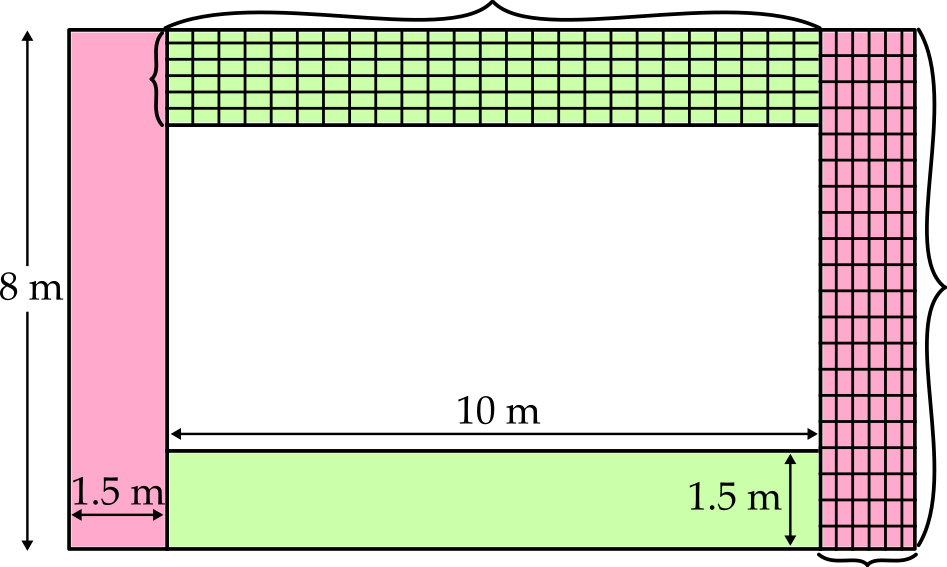
      Two side rectangles with dimensions 8 metres by 1.5 metres and top and bottom rectangles with dimensions 10 metres by 1.5 metres. The top rectangle and one of the side rectangles are each covered by a grid of paving stones.

      • In the top area: \(10 \div 0.4=25\), so \(25\) paving stones placed end to end (with their short sides touching) will span the length of the area.

      • In the top area: \(1.5 \div 0.25=6\), so \(6\) paving stones placed side by side (with their long sides touching) will span the width of the area.

      • In a side area: \(8 \div 0.4=20\), so \(20\) paving stones placed end to end (with their short sides touching) will span the length of the area.

      • In a side area: \(1.5 \div 0.25=6\), so \(6\) paving stones placed side by side (with their long sides touching) will span the width of the area.

      The paving stones may look a bit unusual, since they are placed in different directions so won’t line up at the corners of the pool. However, the 1.5 m width is only evenly divisible by 0.25 m, not by 0.4 m, so for no waste, we’re stuck with a solution where the paving stones are not all in the same direction.