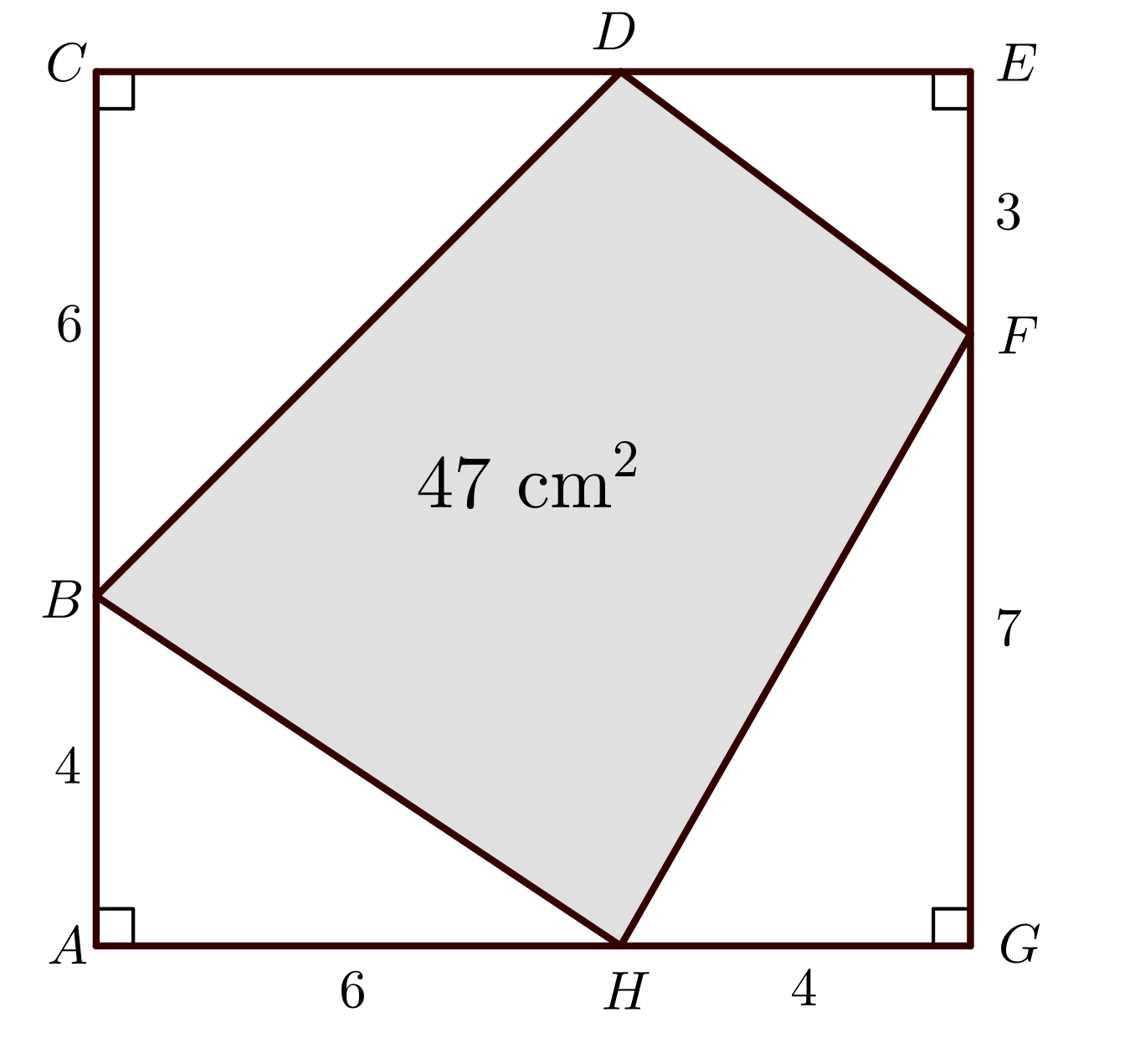
Quadrilateral \(BDFH\) is constructed so that each vertex is on a different side of square \(ACEG\). Vertex \(B\) is on side \(AC\) so that \(AB=4\text{ cm}\) and \(BC=6\text{ cm}\). Vertex \(F\) is on \(EG\) so that \(EF=3\text{ cm}\) and \(FG=7\text{ cm}\). Vertex \(H\) is on \(GA\) so that \(GH=4\text{ cm}\) and \(HA=6\text{ cm}\). The area of quadrilateral \(BDFH\) is \(47\text{ cm}^2\).
The fourth vertex of quadrilateral \(BDFH\), labelled \(D\), is located on side \(CE\) so that the lengths of \(CD\) and \(DE\) are both positive integers.
Determine the lengths of \(CD\) and \(DE\).