Problem
A family has decided that they want to have a pool installed in their backyard. The city they live in has a by-law which states, “No pool may occupy more than \(20\%\) of the total area of the backyard in which it is to be installed.”
Their backyard is rectangular and measures \(24\) m by \(18\) m. The family creates a design in which they divide their backyard into a \(3\) by \(3\) grid of nine identical rectangles. The pool will be circular with the circumference of the pool passing through the four vertices of the middle rectangle. The middle rectangle will be completely covered by the pool. The distance across the pool through its centre will equal the length of the diagonal of the middle rectangle. Their plan is illustrated on the diagram below.
Should their plan be approved by the city?

You may find the following useful:
The Pythagorean Theorem states, “In a right-angled triangle, the square of the length of hypotenuse (the side opposite the right angle) equals the sum of the squares of the lengths of the other two sides.”
In the right-angled triangle shown, \(c\) is the hypotenuse and
\[c^2=\textcolor{red}{a^2}+\textcolor{blue}{b^2}\]

Solution
The dimensions of the backyard are \(24\) m by \(18\) m, so the area of the entire backyard is \(24\times 18=432\text{ m}^2\). To comply with the by-law, the area of the pool cannot be more than \(20\%\) or \(\frac{1}{5}\) of the total area of the backyard.
That is, the area cannot exceed \(\frac{1}{5}\) of \(432\), which is equal to \(\frac{1}{5}\times 432=86.4\text{ m}^2\).
Since we know the length of the backyard is \(24\) m and the backyard is \(3\) rectangles long, the length of one rectangle is \(24\div 3=8\) m. Similarly, since we know the width of the backyard is \(18\) m and the backyard is \(3\) rectangles across, the width of one rectangle is \(18\div 3=6\) m.
Two adjacent sides of the middle rectangle and a diagonal form a right-angled triangle. Let \(d\) represent the length of the hypotenuse of the right-angled triangle with sides \(8\) m and \(6\) m. We know that \(d\) is also the length of the diameter of the pool. Using the Pythagorean Theorem,
\[\begin{aligned} d^2&=&8^2+6^2\\ &=&64+36\\ &=&100\\ d&=&\sqrt{100}\text{, since }d>0\\ d&=&10\text{ m}\end{aligned}\]
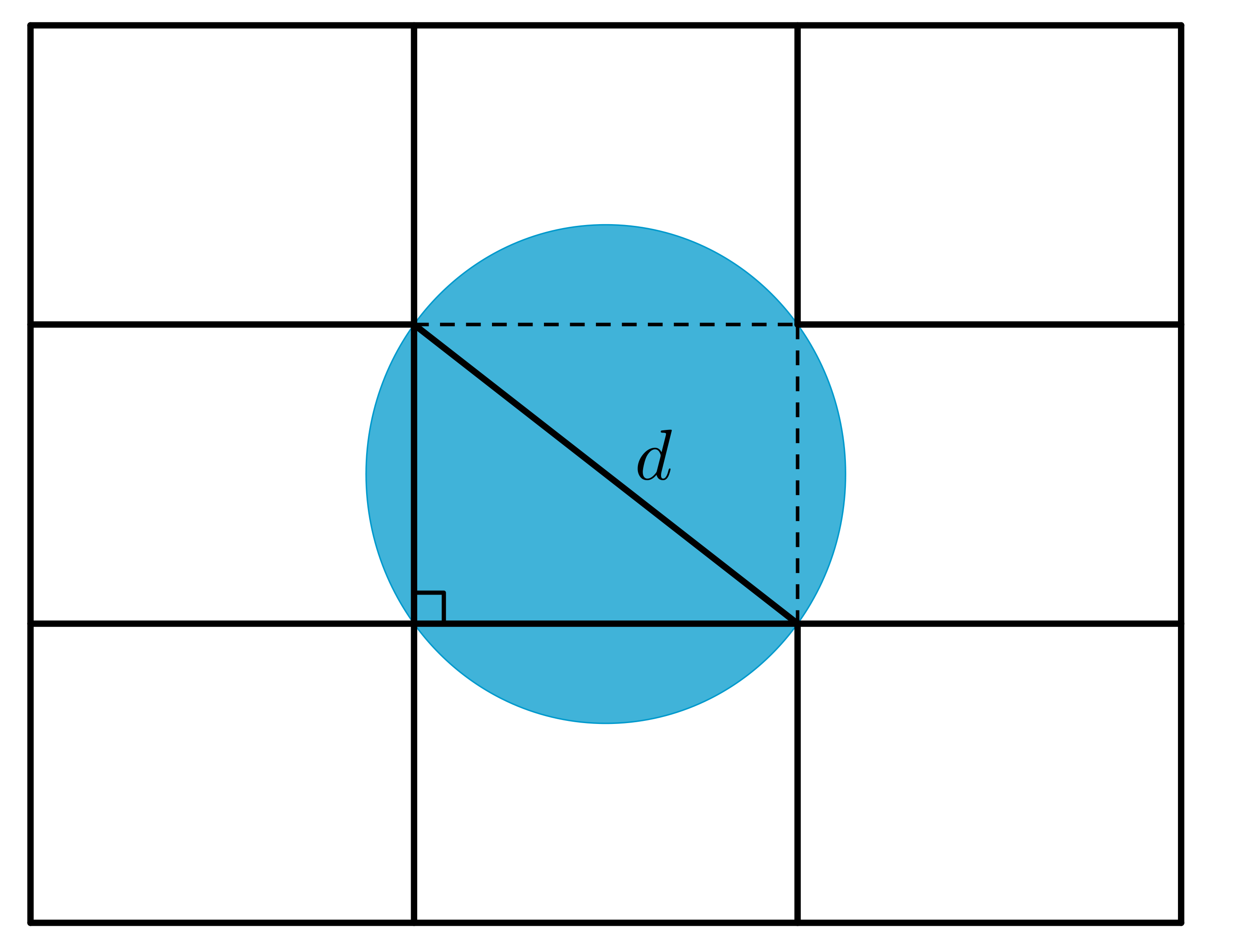
Therefore, the diameter of the pool is \(10\) m, so it follows that the radius of the pool will be \(10\div 2=5\) m.
The area of the pool can be calculated using the formula \(A=\pi r^2\) so \(A=\pi \times (5)^2=25\pi\approx 78.5\text{ m}^2\). Since \(78.5<86.4\), the area of the pool is less than one-fifth of the total area of the backyard.
Therefore, their plan should be approved.
