Solution

CEMC Banner

Problem of the Week

Problem C and Solution

A Path Using Math

Problem

A landscaper needs to fill a path measuring 2 feet by 6 feet with patio stones. The patio stones are each 1 foot by 2 feet, so the landscaper calculates that she will need 6 of them.
Before arranging the patio stones, the landscaper wants to look at all of her options. She cannot cut or overlap the stones, and they all must fit inside the path area without any gaps. Two possible arrangements of the stones are shown below. How many different arrangements are there in total?

One possible arrangement of six, 1 by 2 rectangles filling a 2 by 6 rectangle. There is one rectangle with a vertical orientation, followed a pair of rectangles with a horizontal orientation one on top of the other, followed by one more rectangle placed vertically, followed by another pair of rectangles placed horizontally. Another possible arrangement consisting of two vertical rectangles side by side, followed by a pair of horizontal rectangles one on top of the other, followed by two more vertical rectangles side by side.

Solution

Let’s consider the ways that the patio stones can be arranged. We will imagine we are looking at the path from the side, just like in the images shown in the question. First, notice that there must always be an even number of patio stones that have a horizontal orientation, because they must be placed in pairs.

All patio stones are vertical (and none are horizontal)
This can be done in only one way.
Four patio stones are vertical and two are horizontal
There could be 0, 1, 2, 3 or 4 vertical stones to the right of the horizontal stones. So there are 5 ways that four patio stones are vertical and two are horizontal.
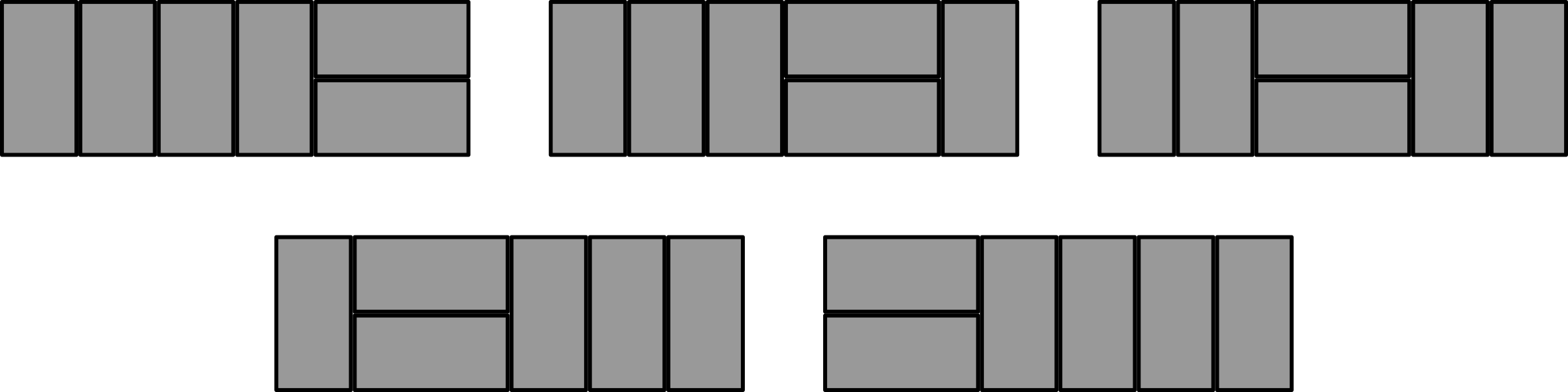
Two patio stones are vertical and four are horizontal
We need to consider sub cases:
- Case 1: There are no vertical stones between the horizontal stones.
  There could be 0, 1 or 2 vertical stones to the right of the horizontal stones. So there are 3 ways that two patio stones are vertical and four are horizontal when there are no vertical stones between the horizontal stones.
- Case 2: There is one vertical stone between the horizontal stones.
  There could be 0 or 1 vertical stones to the right of the rightmost horizontal stones. So there are 2 ways that two patio stones are vertical and four are horizontal when there is one vertical stone between the horizontal stones.
- Case 3: There are two vertical stones between the horizontal stones.
  There cannot be any vertical stones to the right of the rightmost horizontal stones, since all the vertical stones are between the horizontal stones. So there is 1 way that two patio stones are vertical and four are horizontal when there are two vertical stones between the horizontal stones.
All patio stones are horizontal
This can be done in only one way.

Therefore, there are a total of \(1+5+(3+2+1) + 1 = 13\) different arrangements of the patio stones.