Problem of the Week
Problem C and Solution
Penned In

Problem

A square enclosure, labelled \(ABCD\), is sketched out on a piece of graph paper.

Three of the vertices of the square \(ABCD\) are located at \(A(0,3)\), \(B(4,0)\), and \(C(7,4)\).

Determine the area of the square enclosure.

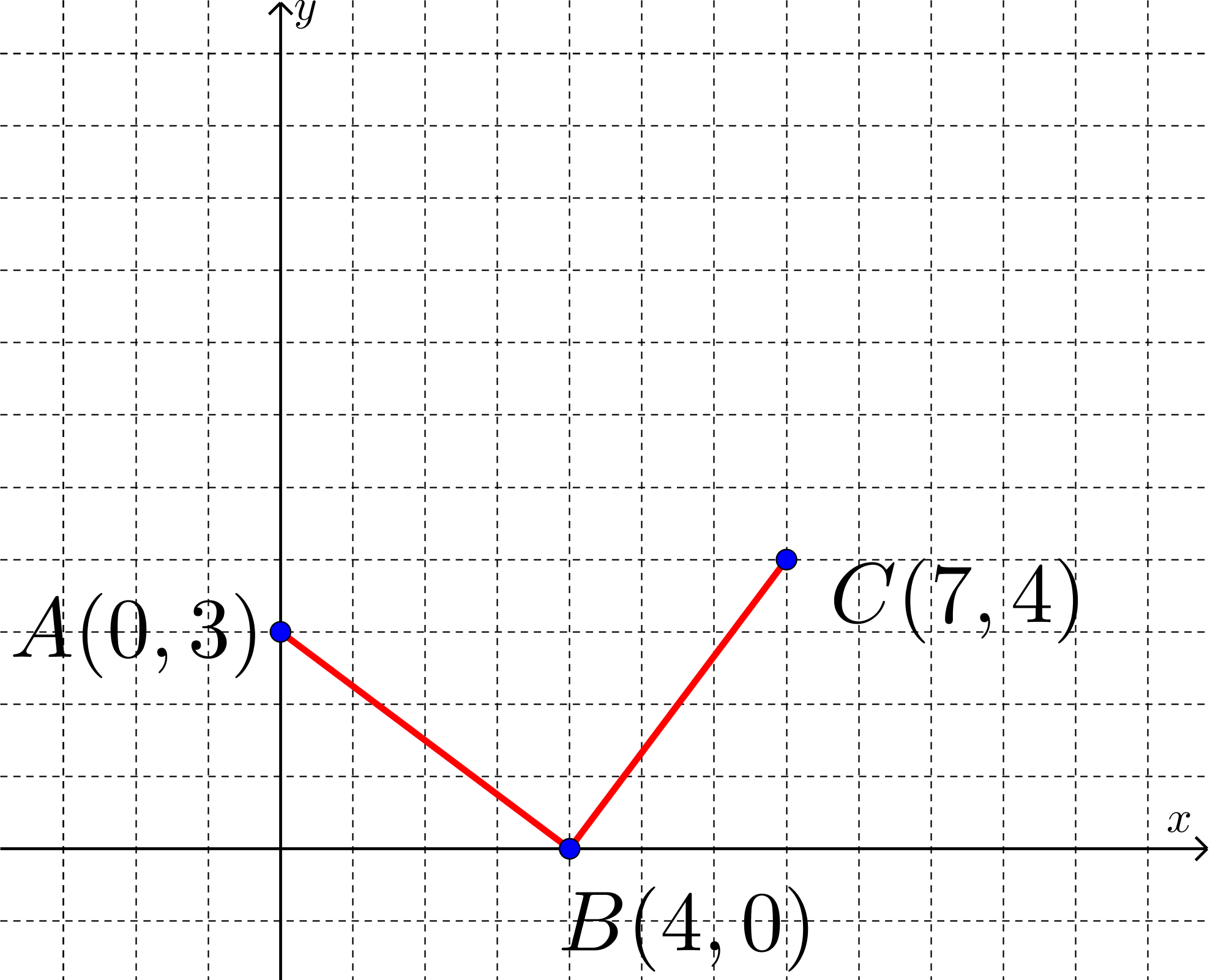
Solution

Solution 1

In this solution we will determine the area of \(ABCD\) without using the Pythagorean Theorem.

We will first determine the coordinates of the fourth vertex \(D\). To do so, observe that to get from \(A\) to \(B\), you would go down \(3\) units and right \(4\) units. To get from \(B\) to \(C\), you move \(3\) units to the right and then \(4\) units up. Continuing the pattern, going up \(3\) units and left \(4\) units, you get to \(D(3,7)\). Continuing, as a check, go left \(3\) units and down \(4\) units, and you arrive back at \(A\). The coordinates of \(D\) are \((3,7)\).

Draw a box with horizontal and vertical sides so that each vertex of the square \(ABCD\) is on one of the sides of the box. This creates a large square with sides of length \(7\) containing four congruent triangles and square \(ABCD\). Each of the triangles has a base \(4\) units long and height \(3\) units long.

\[\begin{aligned} \text{Area }ABCD&=\text{Area of Large Square}-4\times \text{Area of One Triangle}\\ &=\text{Length}\times \text{Width}-4\times(\mbox{Base}\times \text{Height}\div 2)\\ &=7\times 7 - 4\times (4\times 3 \div 2)\\ &=49-4\times 6\\ &=49-24\\ &=25\end{aligned}\]

Therefore, the area of the enclosure is \(25\) units\(^2\).

Solution 2

In this solution we will determine the area of \(ABCD\) using the Pythagorean Theorem.

Since \(ABCD\) is a square, it is only necessary to find the length of one side. We can determine the area by squaring the length of the side.

Label the origin \(O\).
\(OA\), the distance from the origin to point \(A\) on the \(y\)-axis, is \(3\) units. \(OB\), the distance from the origin to point \(B\) on the \(x\)-axis, is \(4\) units. Since \(A\) lies on the \(y\)-axis and \(B\) lies on the \(x\)-axis, \(OAB\) forms a right-angled triangle.

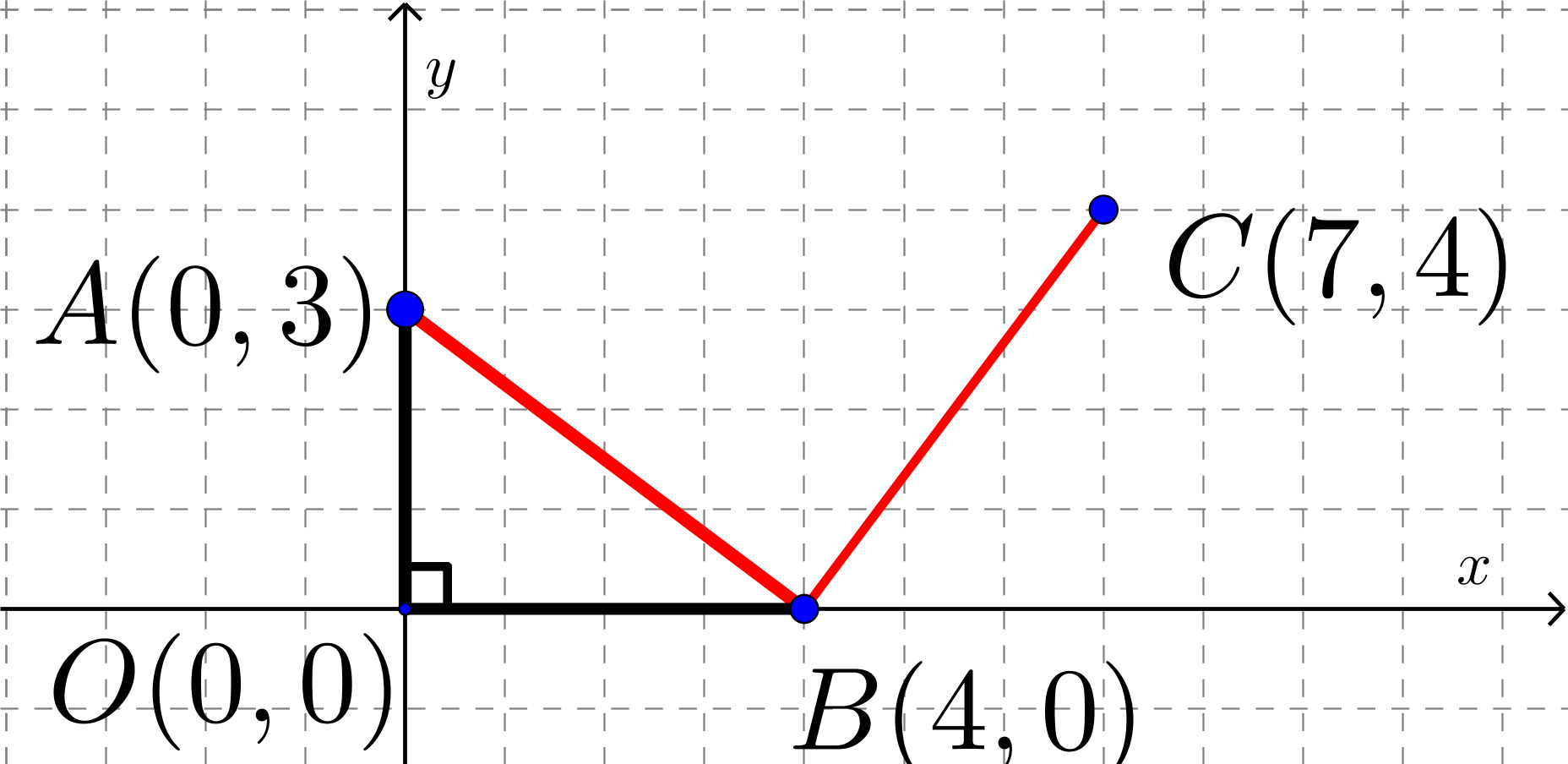
Using the Pythagorean Theorem in right-angled \(\triangle OAB\), we can find \(AB^2\) which is \(AB \times AB\), the area of the square.

\[\begin{aligned} AB^2&=OA^2+OB^2\\ &=3^2+4^2\\ &=9+16\\ &=25\end{aligned}\]

Therefore, the area of the enclosure is \(25\) units\(^2\).