Problem of the Week
Problem D and Solution
Not as Easy as 1, 2, 3
Problem
Zephaniah places the numbers \(1\), \(2\), and \(3\) in the circles below so that each circle contains exactly one of \(1\), \(2\), and \(3\), and any two circles joined by a line do not contain the same number. He then finds the sum of the numbers in the four circles on the far right. What sums could he achieve?
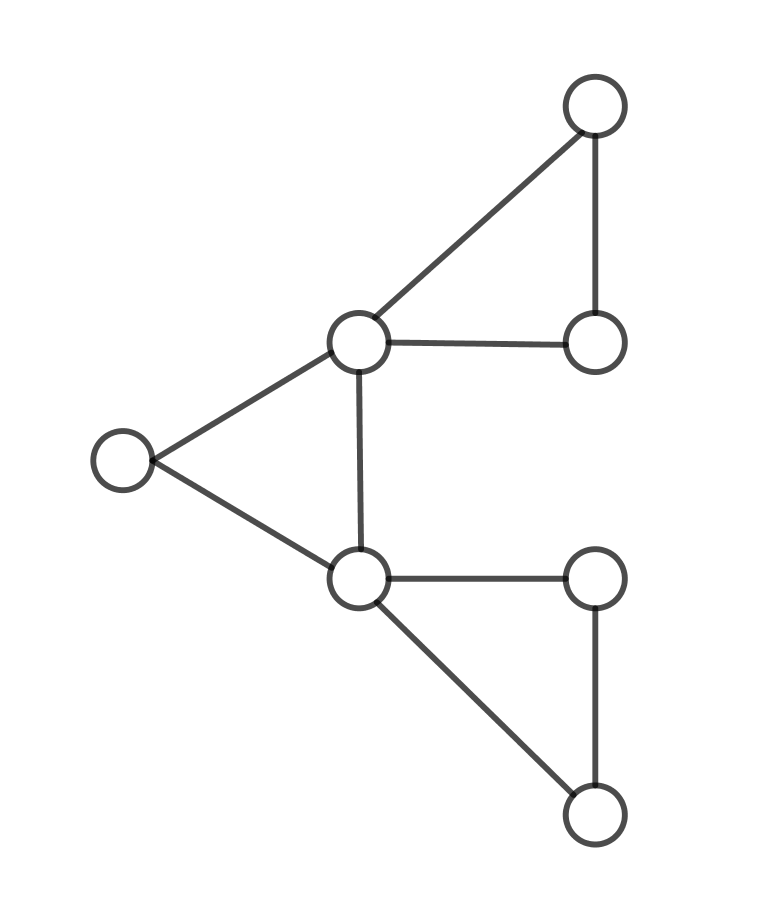
Solution
We will first find the largest possible value for the sum.
First, we note that the four circles on the right cannot all contains \(3\)s, since there are two pairs of circles that are joined. In fact, we cannot have three \(3\)s in those circles, for that means two joined circles will both contain a \(3\). Therefore, we could possibly have two \(2\)s and two \(3\)s, as shown below.

However, this would force the middle two circles to each contain a \(1\). Since these circles are joined by a line, this is not possible. Therefore, the sum of the four circles on the right cannot be \(10\).

However, we can fill in all the circles so that the sum of the four circles on the right is \(9\).

Therefore the largest possible sum is \(9\).
We will now find the smallest possible sum.
We can use similar reasoning to show that the smallest possible sum is \(7\).
The four right circles cannot contain all \(1\)s or three \(1\)s. There could possibly be a \(1\) and \(2\) in the top two circles to the right and a \(1\) and a \(2\) in the bottom two circles to the right. Then the sum of the four numbers to the right would be \(6\). However, this would force the middle two circles to each contain a \(3\). Since these circles are joined by a line, this is not possible. Therefore, the sum cannot be \(6\).
However, we can fill in all the circles so that the sum of the four circles on the right is \(7\).

Therefore, the smallest possible sum is \(7\).
Finally, we can also fill in all the circles so that the sum of the four circles on the right is \(8\).

Therefore, he could achieve a sum of \(7\), \(8\), or \(9\).
