Problem of the Week

Problem E and Solution

Dot Dot Dot

Problem

Ponto forms a triangle using dots, and then puts five of these triangles together to make a star. When he does this, the dots in the bottom corners of each adjacent triangle overlap. An example is shown below.

Ponto creates a sequence of such stars as follows.

• Each triangle in the first star has a row with one dot on top of a row with two dots.

• Each triangle in all subsequent stars has one more row than the triangles in the previous star. This new row is placed at the bottom of each triangle and has one more dot than the row above it.

The first three stars in the sequence are shown. They have 10, 25, and 45 dots showing, respectively.

Which star in the sequence will have 20 020 dots showing?

Note:
In solving the above problem, it may be helpful to use the fact that the sum of the first \(n\) positive integers is equal to \(\tfrac{n(n+1)}{2}\). That is, \[1 + 2 + 3 + … + n = \frac{n(n+1)}{2}\]

Solution

We will write an equation to represent the number of dots in each star in the sequence. We know that each star is made of 5 triangles that overlap at the corners. Thus, the total number of dots in each star is equal to \[(\text{number of dots in each triangle})\times 5 - (\text{number of overlapped dots})\] The overlapped dots are circled in the diagram below. They are the dots in the bottom corners of each triangle.

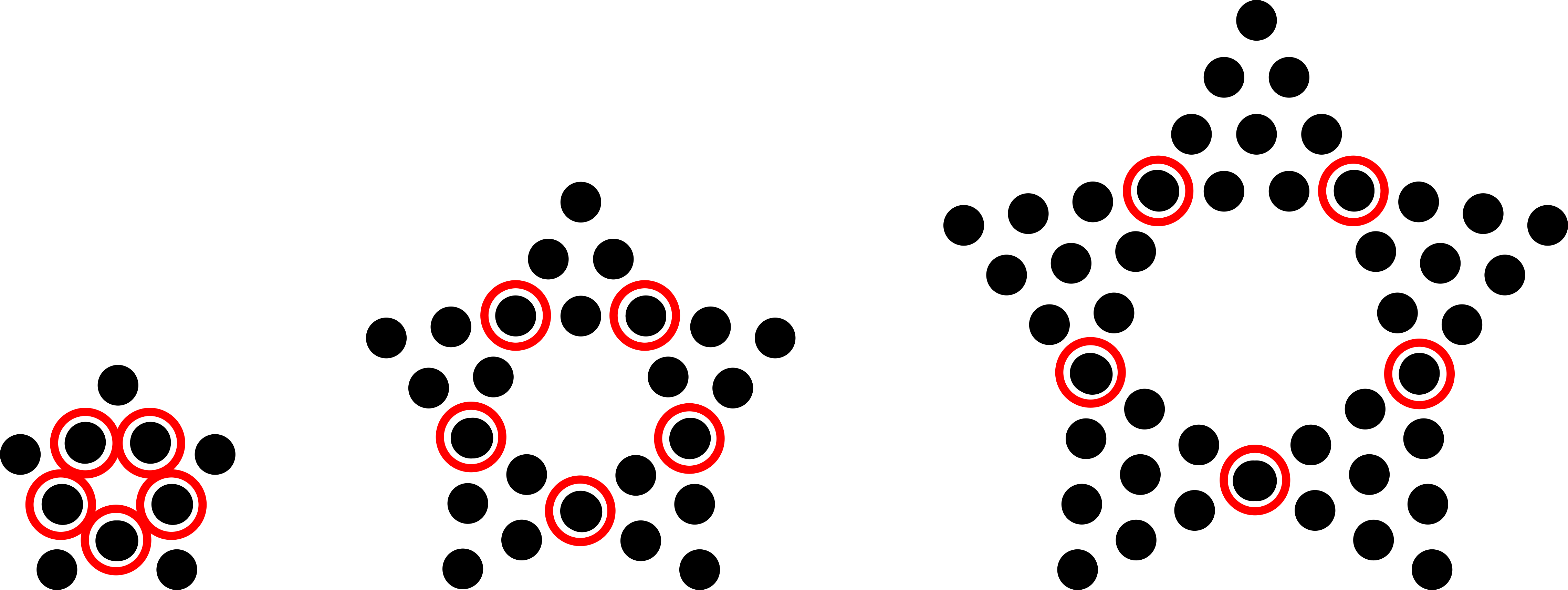
We can see that each star in the sequence will have 5 overlapped dots. So we can simplify our expression for the total number of dots to \[(\text{number of dots in each triangle})\times 5 - 5\] Now let’s look at how many dots are in each triangle.

• The first star has \(1+2=3\) dots in each triangle.

• The second star has \(1+2+3=6\) dots in each triangle.

• The third star has \(1+2+3+4=10\) dots in each triangle.

Following this pattern, we can see that the fourth star would have \(1+2+3+4+5=15\) dots in each triangle. Thus, the \(n^{\text{th}}\) star would have \(1+2+\cdots+n+(n+1)\) dots in each triangle.
We know the sum of the first \(n\) positive integers is \(\dfrac{n(n+1)}{2}\). Thus, the sum of the first \((n+1)\) positive integers is \(\dfrac{(n+1)(n+2)}{2}\). So the \(n^{\text{th}}\) star would have \(\dfrac{(n+1)(n+2)}{2}\) dots in each triangle. If we let \(t_n\) represent the number of dots in the \(n^{\text{th}}\) star in the sequence, then we can write the following equation. \[t_n=\dfrac{(n+1)(n+2)}{2}\times 5 - 5\] We want to know which star has 20 020 dots. This means we want to find the value of \(n\) when \(t_n=20\,020\). \[\begin{aligned} 20020 &= \dfrac{(n+1)(n+2)}{2}\times 5 - 5\\ 20025 &= \dfrac{(n+1)(n+2)}{2}\times 5\\ \dfrac{20025}{5} &= \dfrac{(n+1)(n+2)}{2}\\ 4005 \times 2 &= (n+1)(n+2)\\ 8010 &= n^2 +3n +2\\ 0 &= n^2 +3n -8008\\ 0 &= (n-88)(n+91)\end{aligned}\] Thus \(n=88\), or \(n=-91\). Since \(n\) must be a positive integer, it follows that \(n=88\).
Therefore, the \(88^{\text{th}}\) star has 20 020 dots.
Extension: Show that for any positive integer \(n\), we in fact have \[1 + 2 + 3 + … + n = \dfrac{n(n+1)}{2}\]