Problem of the Week

Problem E and Solution

Rock Out

Problem

Sameer likes playing rock paper scissors so much that he started a club at his school. At every club meeting, each person plays rock paper scissors against each of the other people at the meeting the same number of times.
There were 40% more people at the second club meeting than the first. The total number of rock paper scissors matches played at the second meeting was twice the number of matches played at the first meeting. The number of matches each person plays against each of the other people at the meeting stays the same from meeting to meeting.
How many people were at the first meeting?

Solution

Let \(p\) represent the number of people at the first meeting. Then the number of people at the second meeting is \(1.4p\). Note that both \(p\) and \(1.4p\) must be positive integers.
We need to first establish how many games are played. Suppose there were 4 people (\(A, B, C, \text{ and } D\)), and each person played against every other person once, as shown below.

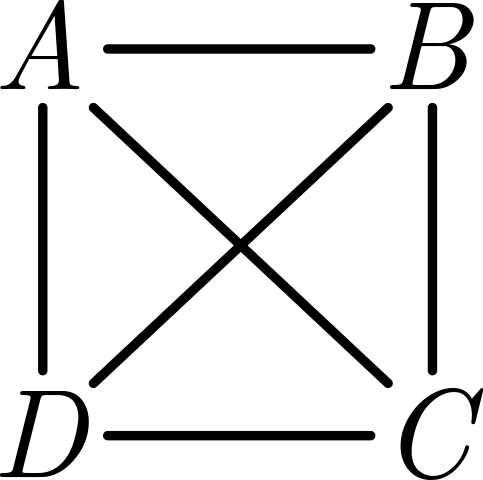
We can see there would be 6 matches played (\(AB\), \(AC\), \(AD\), \(BC\), \(BD\), and \(CD\)). This is easy to see in a small diagram, but as the number of people and matches increase, the diagrams become hard to read, so we need to find a general solution.
Often, when counting something like this we “double-count” by mistake. We think that because there are 4 people and each person plays the 3 other people, that means there are \(4\times 3=12\) matches in total. However, we have counted each match twice, so we need to divide the result by 2. So if there were 4 people, with each person playing every other person once, there would be \(\frac{4\times 3}{2}=6\) matches played in total.
In general, if there are \(p\) people and each person plays against every other person once, there would be \(\frac{p(p-1)}{2}\) matches played in total. If each person plays against every other person \(n\) times, the total number of matches would need to be multiplied by \(n\), to obtain \(n\left(\frac{p(p-1)}{2}\right)\). This represents the total number of matches at the first meeting. Now in the second meeting, the number of people is \(1.4p\), so the total number of matches in the second meeting would be \[n\left(\frac{1.4p(1.4p-1)}{2}\right)\]
We know that the number of matches played at the second meeting is twice the number of matches played at the first meeting. So,

\[n\left(\frac{1.4p(1.4p-1)}{2}\right)=2\left[ n\left(\frac{p(p-1)}{2}\right)\right]\]

Dividing both sides by \(\frac{n}{2},\ n\neq 0\), this simplifies to \[1.4p(1.4p-1)=2p (p-1)\]

Dividing both sides by \(p,\ p\neq 0\), this simplifies to

\[\begin{aligned} 1.4(1.4p-1)&=2 (p-1)\\ 1.96p-1.4&=2p-2\\ 0.6&=0.04p\\ 15&=p\end{aligned}\]

Therefore, there were 15 people at the first meeting.