CEMC Banner

Problem of the Week
Problem E
Stand in a Circle

The numbers from \(1\) to \(17\) are arranged around a circle. One such arrangement is shown.

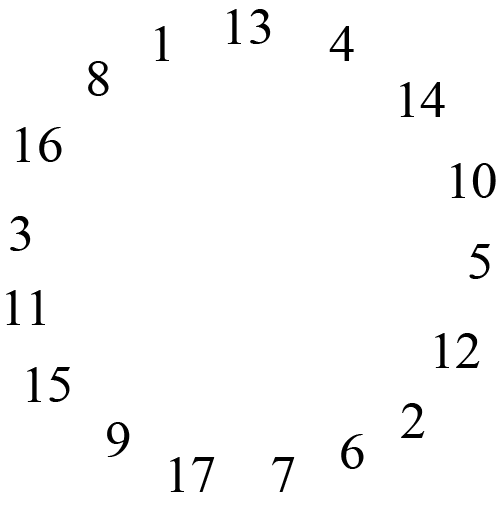
The seventeen numbers are arranged like the numbers on an analogue clock, but placed in a seemingly random order: 13, 4, 14, 10, 5, and so on.

Explain why every possible arrangement of these numbers around a circle must have at least one group of three adjacent numbers whose sum is at least \(27\).

Note:
In solving the above problem, it may be helpful to use the fact that the sum of the first \(n\) positive integers is equal to \(\tfrac{n(n+1)}{2}\). That is, \[1 + 2 + 3 + … + n = \frac{n(n+1)}{2}\]