
Knitting is a process of making rows of stitches out of yarn. To knit a rectangular shape, the number of stitches in each row is always the same. However, to knit different shapes, the number of stitches in each row can be increased or decreased as you work through the pattern.
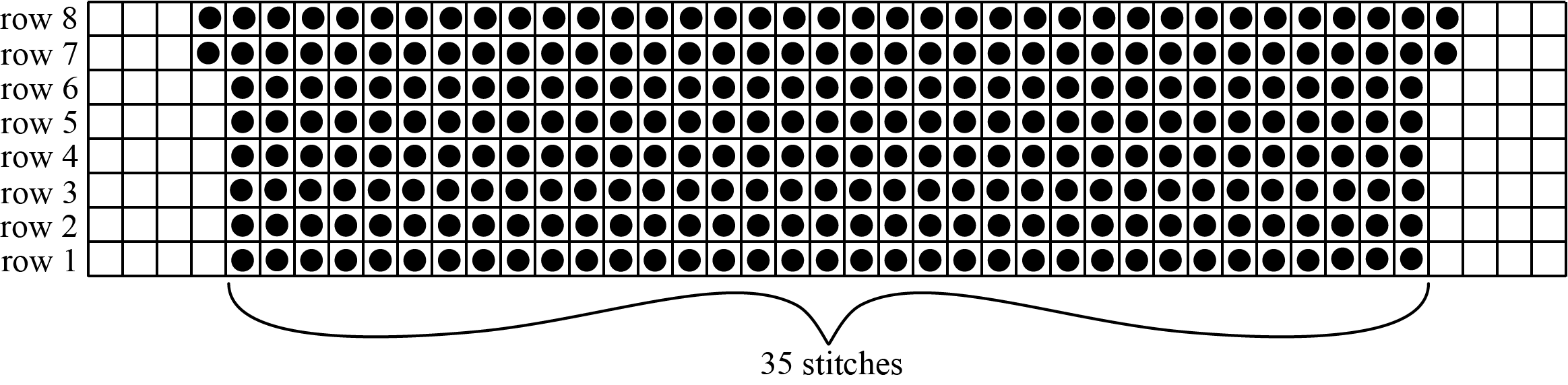
A particular pattern starts with \(35\) stitches in the first row. After every \(6\) rows, \(2\) more stitches are added to the row; one at the beginning and one at the end. So, the \(7\)th row would have \(37\) stitches, and the \(13\)th row would have \(39\) stitches. The first \(8\) rows of the knitting pattern are shown below, with dots representing the stitches. Note that knitting patterns are read from the bottom to the top.

If we follow this pattern, we will create an item that resembles a trapezoid.
How many stitches will be in the \(20\)th row of the pattern?
The length of our finished item is the distance from the first row to the last row. Our finished item will have a length of \(30\) cm. If every \(6\) rows of knitting add \(3\) cm of length, how many rows will there be in total?
How many stitches will be in the last row found in part (b)?

We can make a table showing the number of stitches in each row as we follow the pattern.
| Rows | Number of Stitches |
|---|---|
| \(1 - 6\) | \(35\) |
| \(7 - 12\) | \(37\) |
| \(13 - 18\) | \(39\) |
| \(19 - 24\) | \(41\) |
Since \(20\) is between \(19\) and \(24\), there will be \(41\) stitches in the \(20\)th row.
We can make a table showing the row number and the length of the item after that row has been knitted. Here we will use skip counting and look at the length after every \(6\)th row.
| Row | Length (in cm) |
|---|---|
| \(6\) | \(3\) |
| \(12\) | \(6\) |
| \(18\) | \(9\) |
| \(24\) | \(12\) |
| \(30\) | \(15\) |
| \(36\) | \(18\) |
| \(42\) | \(21\) |
| \(48\) | \(24\) |
| \(54\) | \(27\) |
| \(60\) | \(30\) |
After \(60\) rows, our finished item will have a length of \(30\) cm.
We can make another table showing the number of stitches in each row, again using skip counting and looking at every \(6\)th row up to row \(60\).
| Row | Number of Stitches |
|---|---|
| \(6\) | \(35\) |
| \(12\) | \(37\) |
| \(18\) | \(39\) |
| \(24\) | \(41\) |
| \(30\) | \(43\) |
| \(36\) | \(45\) |
| \(42\) | \(47\) |
| \(48\) | \(49\) |
| \(54\) | \(51\) |
| \(60\) | \(53\) |
The \(60\)th row will have \(53\) stitches.