Sam is making square picture frames using popsicle sticks. He has one box of \(50\) popsicle sticks and wants to make \(13\) frames.
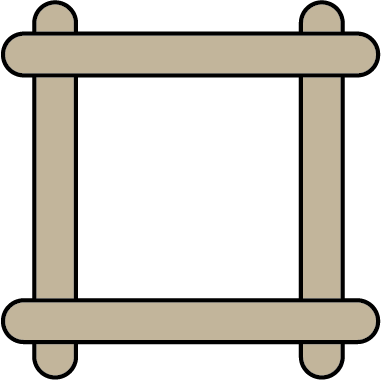
Sam plans to make individual frames using four popsicle sticks as shown.
Will he have enough popsicle sticks to make \(13\) frames? Justify your answer.
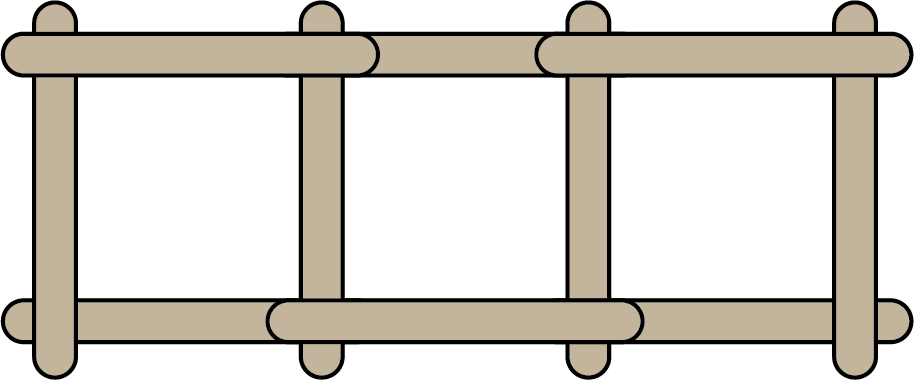
Sam changes his mind and instead of individual frames, he decides to connect the frames in a row. He starts by making a frame using four popsicle sticks, and then uses three popsicle sticks to create another frame attached to this frame. He then uses three more popsicle sticks to create another frame attached to the first two frames, so he has three connected frames, as shown.
Sam plans to continue this process, using three more popsicle sticks for each frame, until he has \(13\) frames connected in a row. Will he have enough popsicle sticks to make \(13\) frames? Justify your answer.
Can you draw another layout of the \(13\) frames that Sam could have built using at most \(50\) popsicle sticks? How many popsicle sticks does your layout use?
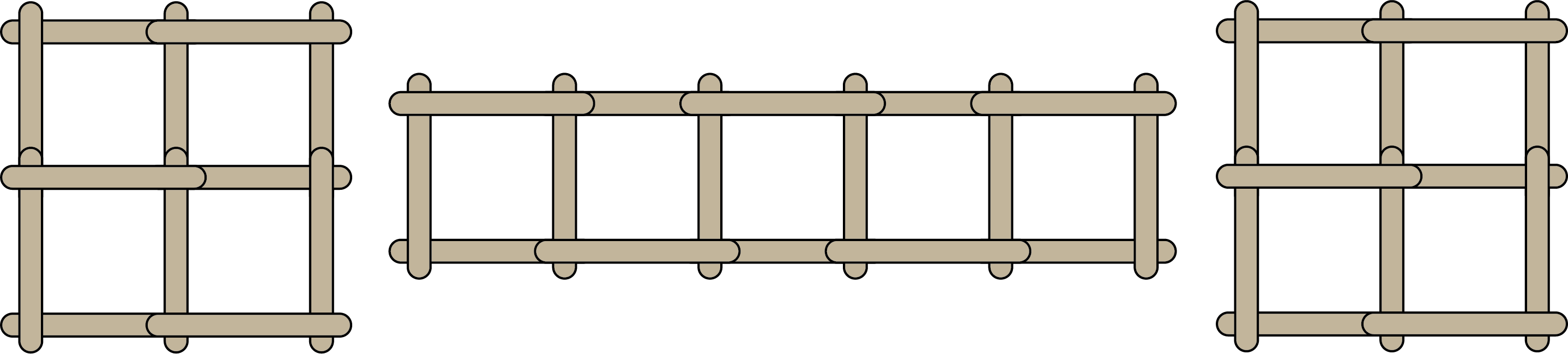
Can you draw a layout of the \(13\) frames that uses fewer than \(35\) popsicle sticks?
Since each frame requires \(4\) popsicle sticks, the total number of popsicle sticks required for \(13\) frames is equal to \(13 \times 4 = 52\).
Alternatively, we could make a table showing the number of frames and the number of popsicle sticks required.
| \(1\) |
\(4\) |
| \(2\) |
\(8\) |
| \(3\) |
\(12\) |
| \(4\) |
\(16\) |
| \(5\) |
\(20\) |
| \(6\) |
\(24\) |
| \(7\) |
\(28\) |
| \(8\) |
\(32\) |
| \(9\) |
\(36\) |
| \(10\) |
\(40\) |
| \(11\) |
\(44\) |
| \(12\) |
\(48\) |
| \(13\) |
\(52\) |
Either way, since it will take \(52\) popsicle sticks to make \(13\) individual frames, Sam will not have enough popsicle sticks to make all the frames.
The first frame uses \(4\) popsicle sticks but the other \(12\) frames use only \(3\) popsicle sticks each. So the total number of popsicle sticks required can be found by adding \(4\) to \(12 \times 3\). Since \(12 \times 3 = 36\), this gives a total of \(4 + 36 = 40\) popsicle sticks.
Alternatively, we could make a table showing the number of frames and the number of popsicle sticks required.
| \(1\) |
\(4\) |
| \(2\) |
\(7\) |
| \(3\) |
\(10\) |
| \(4\) |
\(13\) |
| \(5\) |
\(16\) |
| \(6\) |
\(19\) |
| \(7\) |
\(22\) |
| \(8\) |
\(25\) |
| \(9\) |
\(28\) |
| \(10\) |
\(31\) |
| \(11\) |
\(34\) |
| \(12\) |
\(37\) |
| \(13\) |
\(40\) |
Either way, since it will take \(40\) popsicle sticks to build a row of \(13\) connected frames, Sam will have enough popsicle sticks to make all the frames.
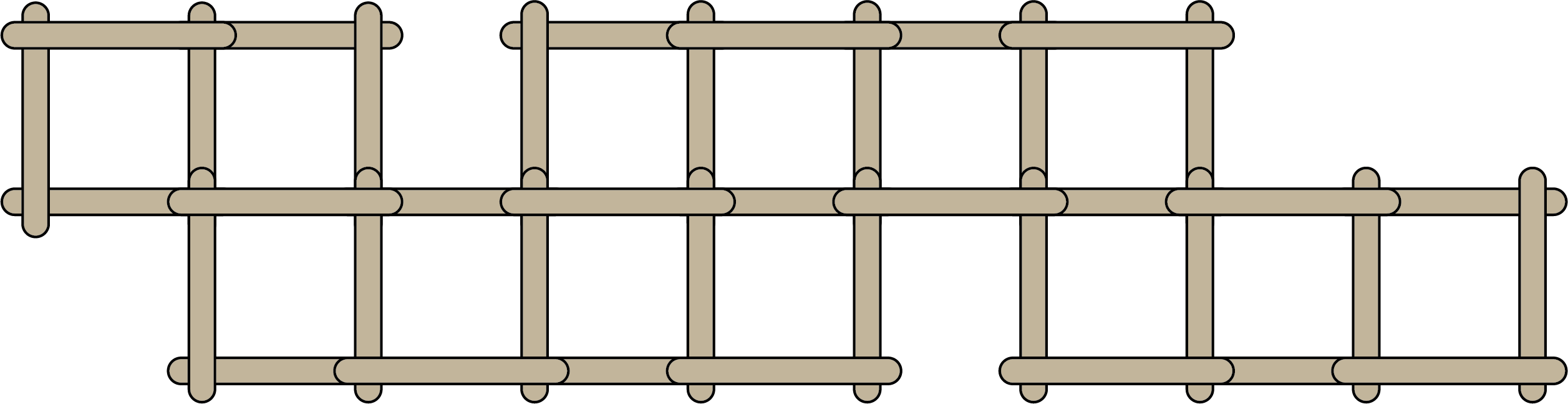
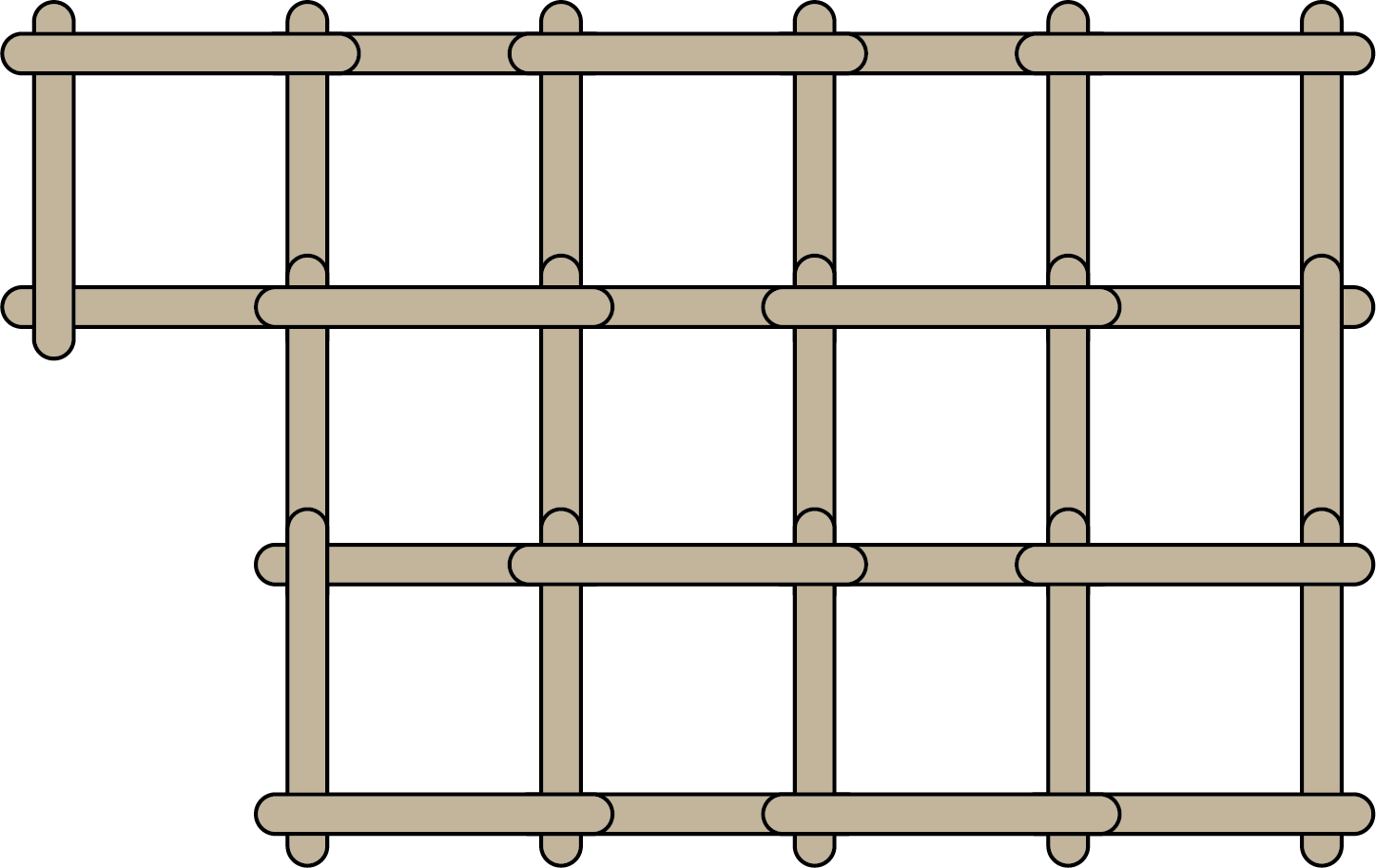
There are many layouts of \(13\) frames you could make using at most \(50\) popsicle sticks. Two examples are shown.
The following layout uses \(39\) popsicle sticks.
The following layout uses \(40\) popsicle sticks.
The most efficient use of popsicle sticks is to share as many sides as possible with other frames. If you connect the frames to form a shape as close as possible to a square, you can make \(13\) frames using only \(34\) popsicle sticks, as shown.