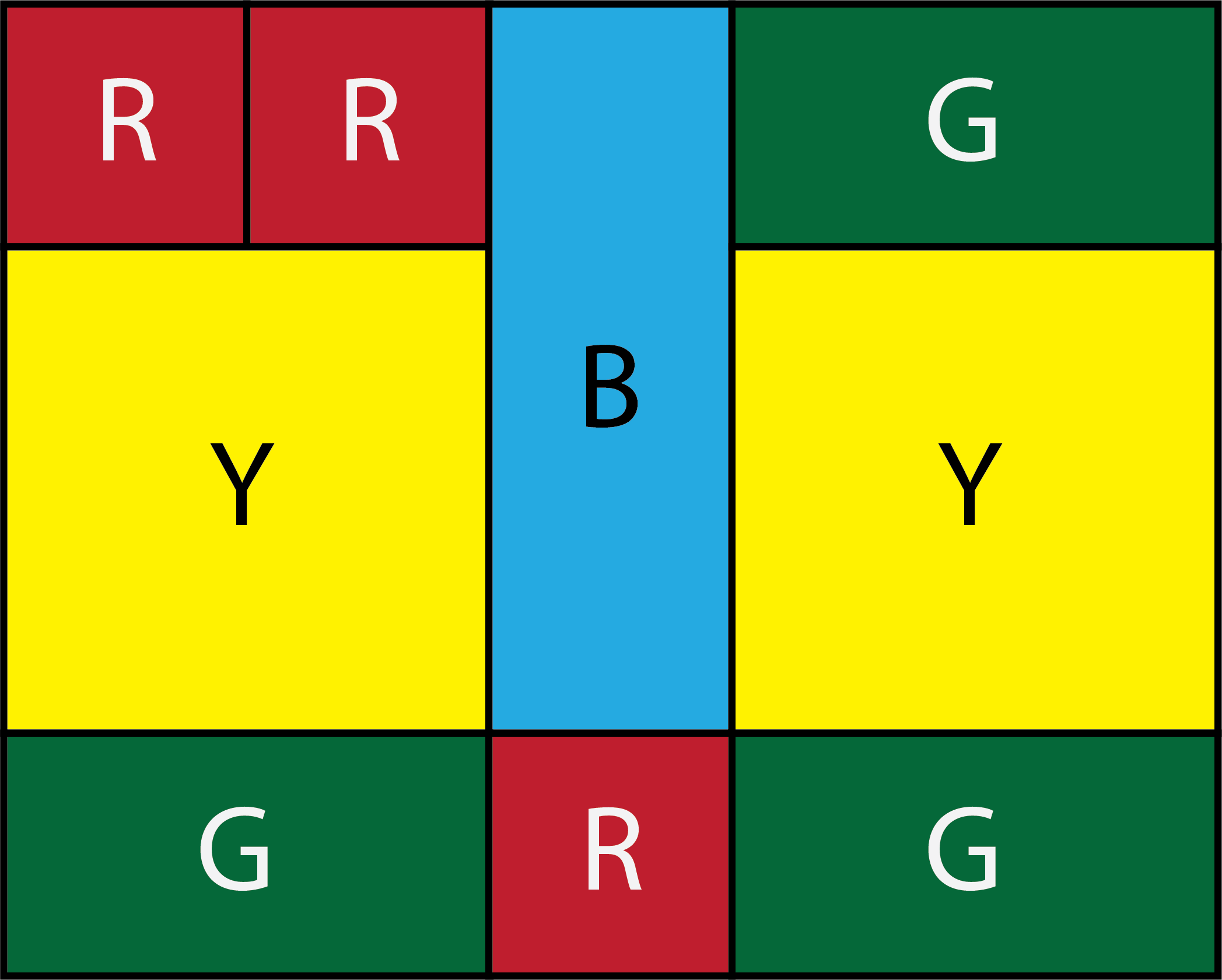

Arvin has red, yellow, green, and blue tiles. The red and yellow tiles are squares, and the green and blue tiles are rectangles. All tiles of the same colour have the same dimensions. Arvin places his tiles next to each other in order to create the following rectangle.

If Arvin wanted to use only red squares to make a rectangle with the same dimensions, how many red squares would he need?
We can see from the diagram that the side length of a yellow square is twice the side length of a red square. This means that if we arrange four red squares, two across and two down, we will form a square with the same dimensions as a yellow square.
We also see from the diagram that the shorter side of a green rectangle is the same length as the side length a red square, and the longer side of a green rectangle is the same length as the side length of a yellow square. Since the side length of a yellow square is twice the side length of a red square, if we arrange two red squares beside each other, we will form a rectangle with the same dimensions as a green rectangle.
From the diagram we see that the shorter side of a blue rectangle is the same length as the side length a red square, and the longer side of a blue rectangle is the same length as the sum of the side length of a yellow square plus the side length of a red square. Since the side length of a yellow square is twice the side length of a red square, if we arrange three red squares in a line, we will form a rectangle with the same dimensions as a blue rectangle.
In summary:
\(1\) yellow square \(= 4\) red squares
\(1\) green rectangle \(= 2\) red squares
\(1\) blue rectangle \(= 3\) red squares
We can create a rectangle with the same dimensions as shown in the diagram by replacing each yellow, green, and blue tile with the equivalent number of red squares.
| Tile Colour | Number in Diagram | Equivalent Number of Red Squares |
|---|---|---|
| yellow | \(2\) | \(2 \times 4 = 8\) |
| green | \(3\) | \(3 \times 2 = 6\) |
| blue | \(1\) | \(1 \times 3 = 3\) |
Including the three red squares in the original diagram, we see that the rectangle can be formed using \(8 + 6 + 3 + 3 = 20\) red squares.