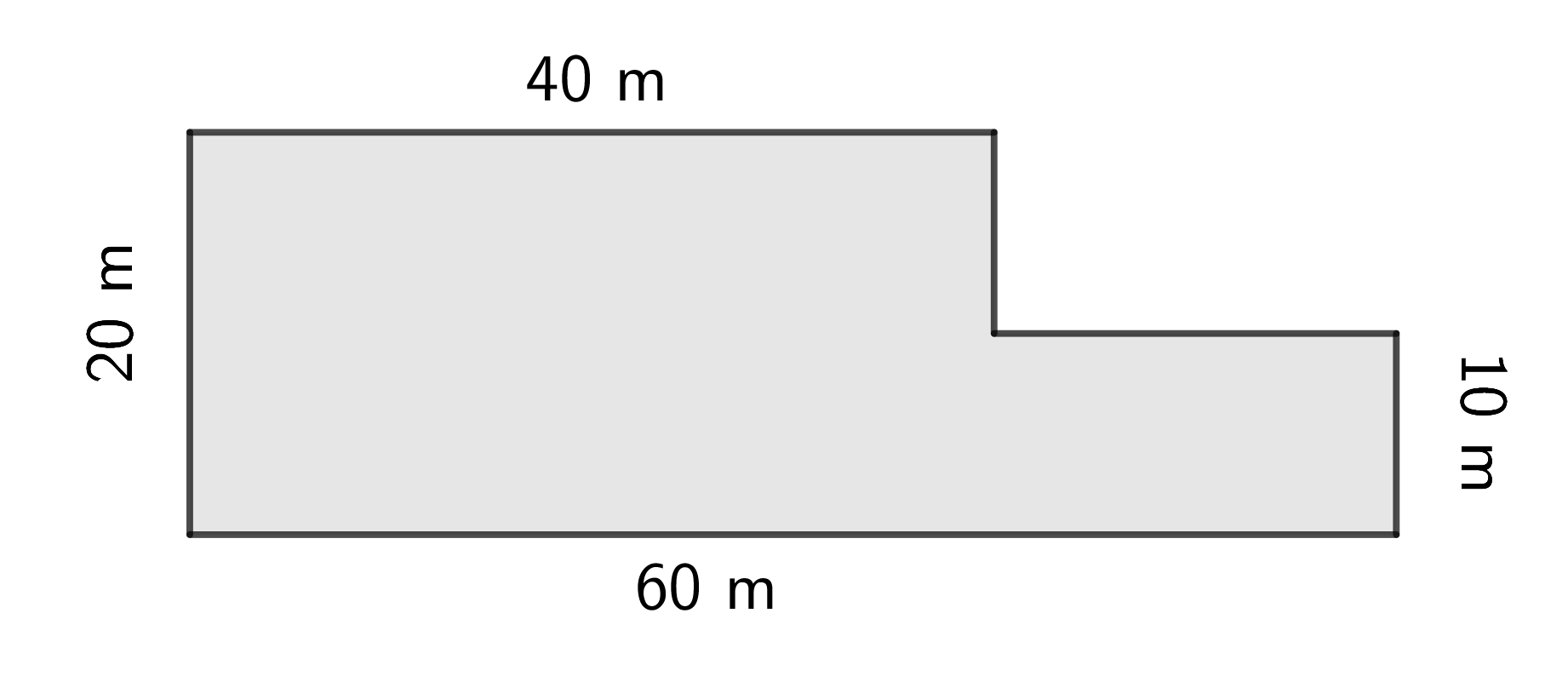

The diagram below shows the shape, and some of the dimensions, of an L-shaped parking lot. All angles in the diagram are right angles.

What is the perimeter of the parking lot?
What is the area of the parking lot?
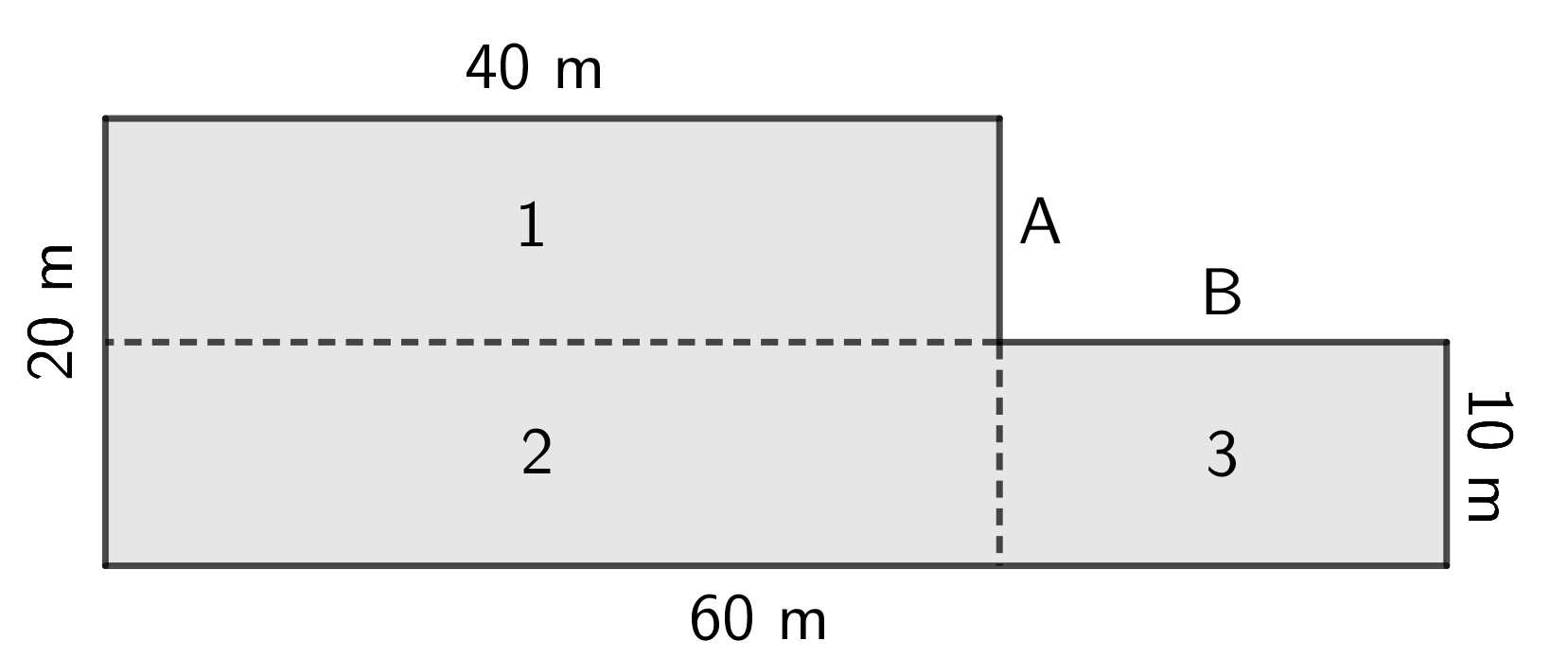
To determine the perimeter and area of the parking lot, we add two dashed lines that extend the sides labelled A and B below. This divides the L-shaped lot into three rectangles, labelled \(1\), \(2\), and \(3\), as shown below.
Since all angles are right angles, we know that the dashed line that is an extension of side B is \(40\) m in length, and the dashed line that is an extension of side A is \(10\) m in length.
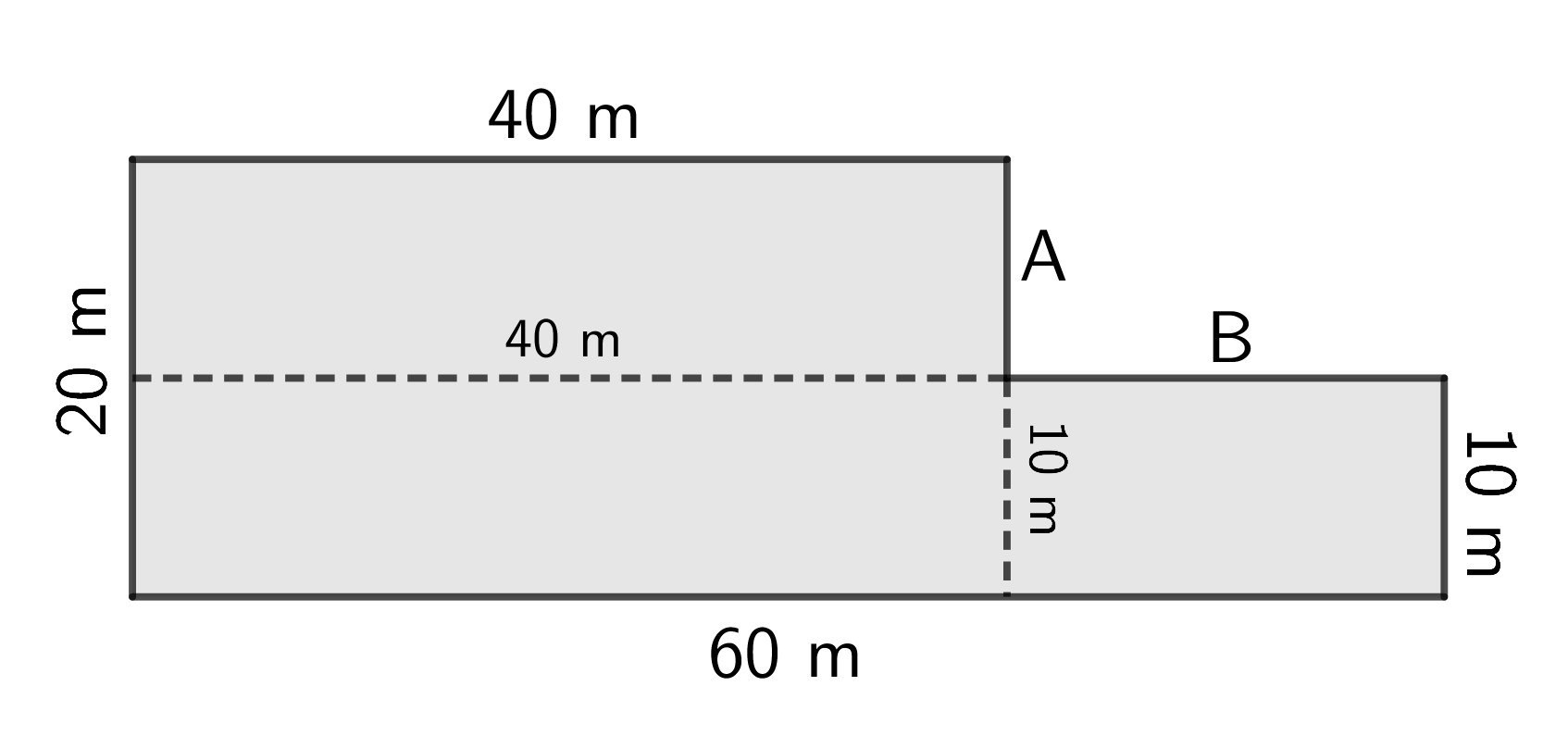
We can now see that the length of side A is \(20 - 10 = 10\) m, and the length of side B is \(60 - 40 = 20\) m. A diagram with all of these dimensions included is shown below.
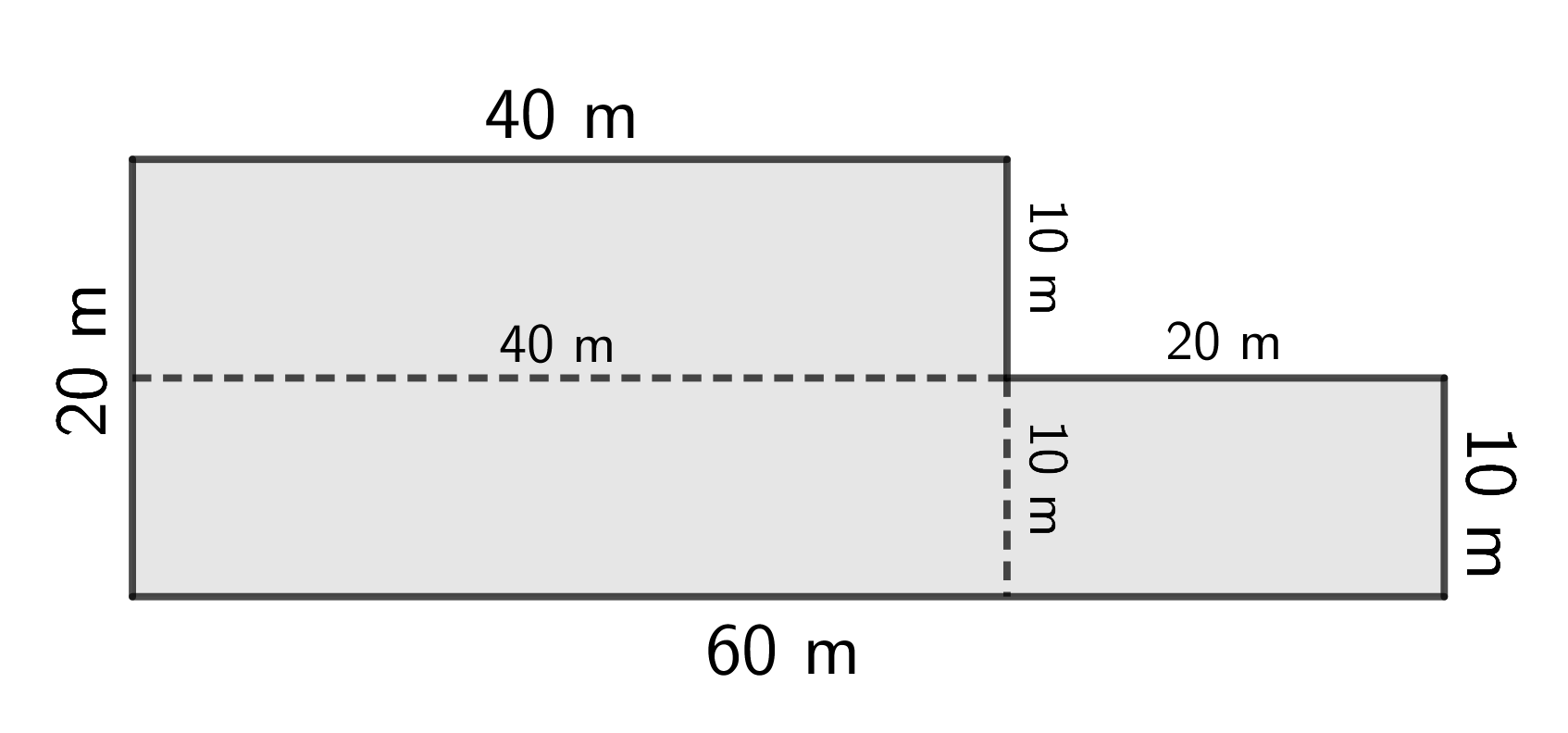
We now have enough information to calculate the perimeter and area of the parking lot.
The perimeter of the parking lot is \(20 + 40 + 10 + 20 + 10 + 60 = 160\) m.
The area of the parking lot is equal to the sum of the areas of the three rectangles, rectangles 1, 2, and 3.
Rectangles 1 and 2 are each \(40~\text{m}\) by \(10~\text{m}\). Therefore, rectangles 1 and 2 each have an area of \(40 \times 10 = 400~\text{m}^2\).
Rectangle 3 is \(20~\text{m}\) by \(10~\text{m}.\) Therefore, rectangle 3 has an area of \(20 \times 10 = 200~\text{m}^2\).
Therefore, the total area of the parking lot is \(400 + 400 + 200 = 1000~\text{m}^2\).
Alternatively, we could divide the diagram into two parts, a \(40~\text{m}\) by \(20~\text{m}\) rectangle and a \(20~\text{m}\) by \(10~\text{m}\) rectangle.
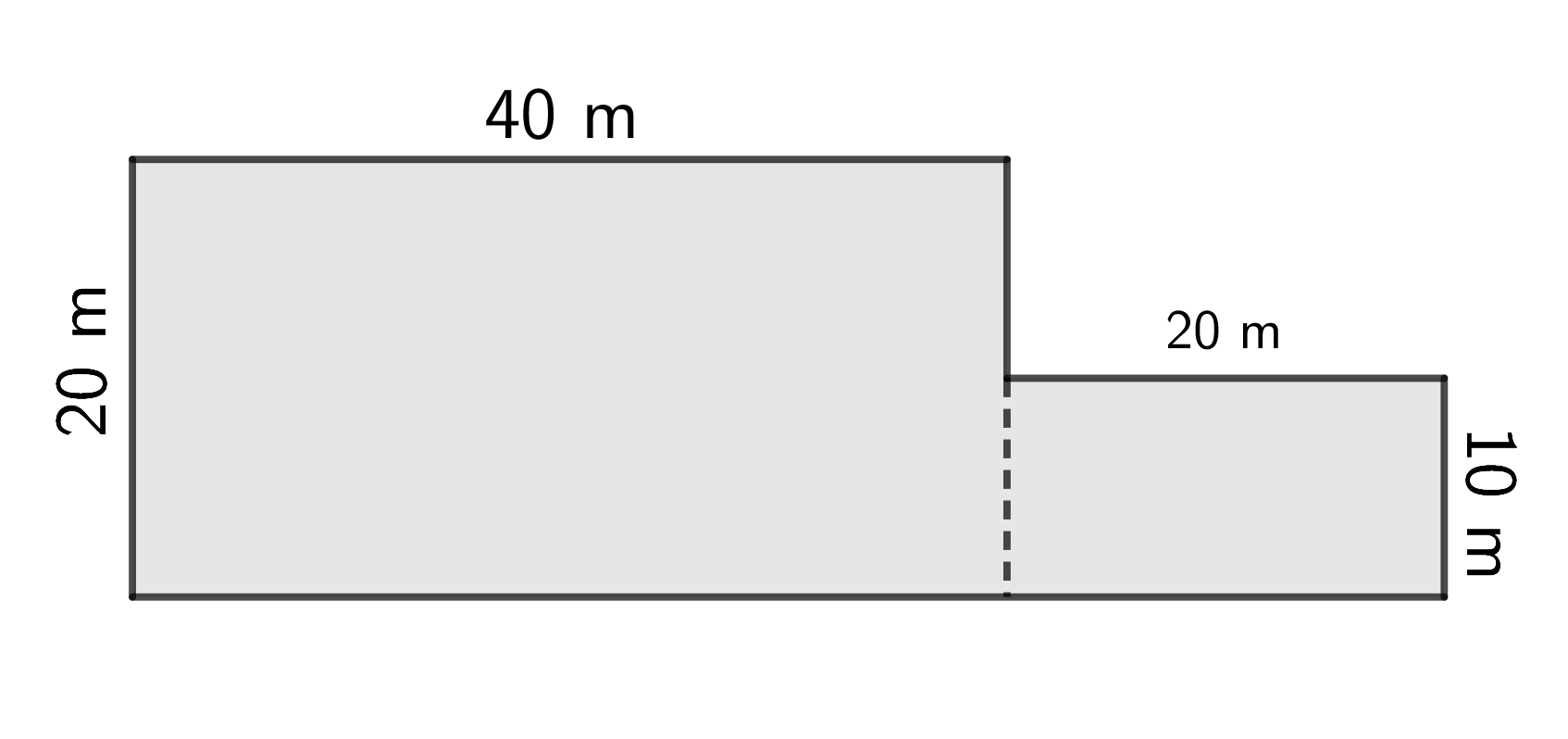
The area of the \(40~\text{m}\) by \(20~\text{m}\) rectangle is \(40 \times 20 = 800~\text{m}^2\).
The area of the \(20~\text{m}\) by \(10~\text{m}\) rectangle is \(20 \times 10 = 200~\text{m}^2\).
Therefore, the total area of the parking lot is \(800 + 200 = 1000~\text{m}^2\).