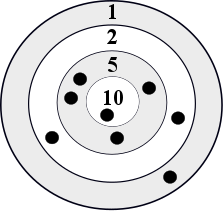


What was the total number of points scored by the two players?
If Ebony’s total score was \(1\) more than Serena’s, what was each person’s score?
What individual shots could each player have had to get their scores?
Whose dart landed in the inner circle?
Since one dart landed in the band worth \(1\) point, two darts landed in the band worth \(2\) points, four darts landed in the band worth \(5\) points, and one dart landed in the inner circle worth \(10\) points, the total number of points scored by the two players was \[1+2+2+5+5+5+5+10=35\]
Since \(35=17+18\), Ebony scored \(18\) points and Serena scored \(17\) points.
Trying all combinations of four shots, we can see that the only way to get a score of \(18\) is as \(1+2+5+10\).
Therefore, Ebony made shots worth \(1\), \(2\), \(5\), and \(10\) points. This means that Serena made shots worth \(2\), \(5\), \(5\), and \(5\) points.
Since the inner circle is worth \(10\) points, then one of Ebony’s darts landed in the inner circle.