CEMC Banner

Problem of the Week
Problem B and Solution
Jumping Jacks with Jym

Problem

Jym’s class has been working on jumping jacks and charting their progress. The mean (average) for the class was determined using each student’s information, giving a value of \(40\) jumping jacks (JJs) per minute.

Over \(10\) days, Jym measured how many jumping jacks he can do in one session, and how long it took him to do them. The tables below show his results.

Day Number of JJs Time taken JJs per minute
\(1\) \(32\) \(58\) s
\(2\) \(32\) \(57\) s
\(3\) \(34\) \(59\) s
\(4\) \(35\) \(57\) s
\(5\) \(40\) \(1\) min \(2\) s
Day Number of JJs Time taken JJs per minute
\(6\) \(42\) \(1\) min \(5\) s
\(7\) \(40\) \(58\) s
\(8\) \(45\) \(1\) min \(2\) s
\(9\) \(46\) \(1\) min
\(10\) \(48\) \(1\) min

  1. Complete the tables by finding Jym's JJs per minute for each day, rounding to the nearest decimal.

  2. Calculate the mean of the values you found in (a). How does this mean for Jym compare to the rest of his class?

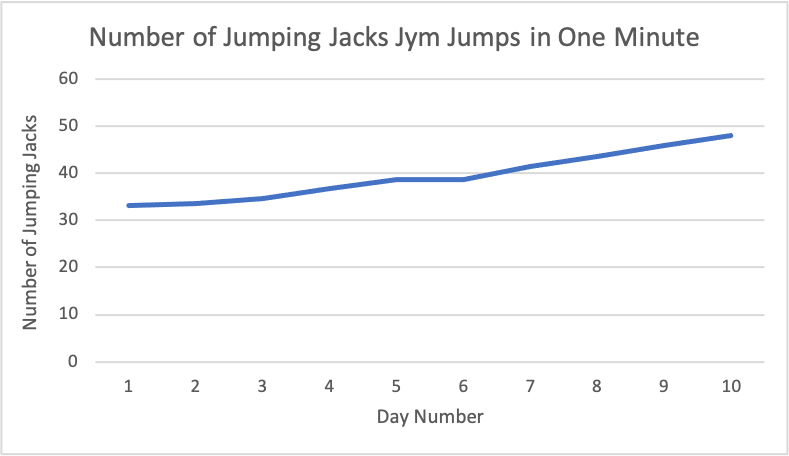
  3. Which type of graph would be most appropriate to show Jym's improvement over time? Create a suitable graph with appropriate labels.

Solution

  1. The completed tables are as follows.

    Day Number of JJs Time taken JJs per minute
    \(1\) \(32\) \(58\) s \(33.1\)
    \(2\) \(32\) \(57\) s \(33.7\)
    \(3\) \(34\) \(59\) s \(34.6\)
    \(4\) \(35\) \(57\) s \(36.8\)
    \(5\) \(40\) \(1\) min \(2\) s \(38.7\)
    Day Number of JJs Time taken JJs per minute
    \(6\) \(42\) \(1\) min \(5\) s \(38.8\)
    \(7\) \(40\) \(58\) s \(41.4\)
    \(8\) \(45\) \(1\) min \(2\) s \(43.5\)
    \(9\) \(46\) \(1\) min \(46\)
    \(10\) \(48\) \(1\) min \(48\)

    Jym’s JJs per minute each day were found by taking his total number of JJs and dividing by the time taken, in seconds, to get the number of JJs per second, and then multiplying this number by \(60\) to get the number of JJs per minute.

    For example, on Day \(1\) Jym jumped \(\dfrac{32}{58}\) JJs per second, which is equivalent to \(\dfrac{32}{58} \times 60 \approx 33.1\) JJs per minute.

  2. Jym’s mean JJs per minute is \[\normalsize\frac{33.1 + 33.7 + 34.6 + 36.8 + 38.7 + 38.8 + 41.4 + 43.5 + 46 + 48}{10} = \frac{394.6}{10} = 39.46 \approx 39.5\] Jym’s mean of \(39.5\) JJs per minute is slightly less than the mean for the class.

  3. The most meaningful graph would be one showing Jym’s average JJs per minute versus time, as a broken line graph (or a bar graph). A broken line graph is shown below.

A graph with title Number of Jumping Jacks Jym Jumps in One Minute. The horizontal axis shows the Day Number. The vertical axis shows the Number of Jumping Jacks where the scale ranges from 0 to 60 counting by tens. The graph shows that the number of jumping jacks in one minute gradually increases from Day 1 to Day 10.