Problem of the Week
Problem B and Solution
Where’s the Audience?

Problem

The Pythagorean Triples are a rock band who recently returned from their second Canadian tour.

1. Information about ticket sales for three of the venues they played at is summarized in the following table.

   Venue	Number of Tickets Available	Number of Tickets Sold
   Olympic Stadium	\(60\,000\)	\(45\,000\)
   Commonwealth Stadium	\(55\,000\)	\(44\,000\)
   BC Place	\(54\,000\)	\(48\,600\)

   For each venue, what percentage of available tickets were sold?

2. Two years ago, the Pythagorean Triples played at the same three venues on their first Canadian tour. For each venue, the percentage of available tickets that were sold is shown in the bar graph below.

   

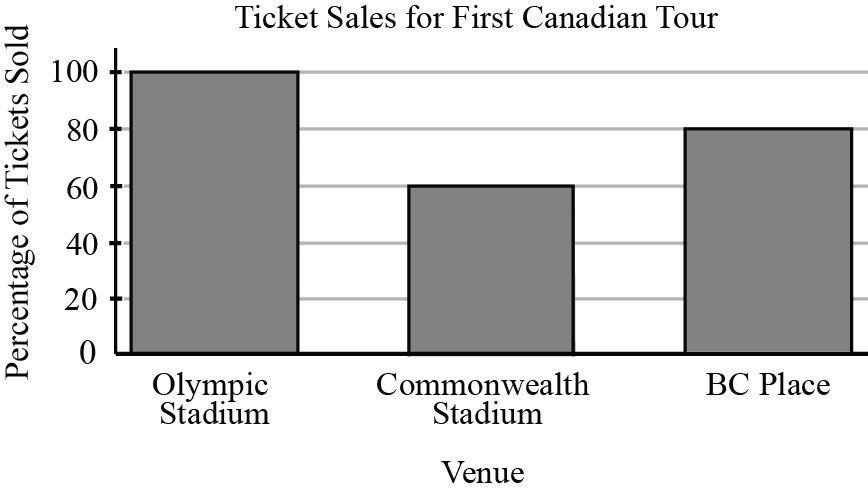
   If the number of tickets available for each venue was the same for both tours, which tour sold more tickets for these three venues combined? Justify your answer.

Solution

1. To calculate the percentage of available tickets that were sold, we divide the number of tickets sold by the number of tickets available, and then multiply by \(100\%\) to convert the decimal to a percentage.

   • Olympic Stadium: \(45\,000\div 60\,000=0.75\), and \(0.75\times 100\%=75\%\).

   • Commonwealth Stadium: \(44\,000\div 55\,000=0.8\), and \(0.8\times 100\%=80\%\).

   • BC Place: \(48\,600\div 54\,000=0.9\), and \(0.9\times 100\%=90\%\).

2. We need to calculate the total number of tickets sold for the three venues for each of the tours.

   • For the second Canadian tour, we can add up the number of tickets sold for each venue in the table from part (a). \[45\,000+44\,000+48\,600=137\,600\]

   • For the first Canadian tour, we first need to use the percentages in the bar graph to calculate the number of tickets sold at each venue. The bar graph shows that \(100\%\) of the available tickets at Olympic stadium were sold, \(60\%\) were sold at Commonwealth Stadium, and \(80\%\) were sold at BC Place.

     • Olympic Stadium: \(100\%\) of \(60\,000\) is \(60\,000\).

     • Commonwealth Stadium: \(60\%\) of \(55\,000\) is equal to \(\dfrac{60}{100}\times 55\,000\) or \(\dfrac{3}{5}\times 55\,000\), which equals \(33\,000\).

     • BC Place: \(80\%\) of \(54\,000\) is equal to \(\dfrac{80}{100}\times 54\,000\) or \(\dfrac{4}{5}\times 54\,000\), which equals \(43\,200\).

     Thus, the total number of tickets sold for the three venues for the first Canadian tour is \[60\,000+33\,000+43\,200=136\,200\]

   Since \(137\,600>136\,200\), it follows that the second Canadian tour sold more tickets for the three venues combined.