
Farmer Holly has a wagon with a wood deck and four tires. When empty, the wagon has a total mass of \(770\) kg. She uses her wagon to transport hay bales in the shape of rectangular prisms. Each hay bale is \(1.4\) m long by \(1.5\) m wide by \(2\) m high, and has a mass of \(300\) kg.
Each of the four tires on the wagon has a maximum load of \(1100\) kg. That is, with each tire an additional \(1100\) kg can be added to the load on the wagon. How many hay bales could Farmer Holly put on her wagon without risking a tire blowout? Don’t forget that the tires are also carrying the load of the wagon itself!
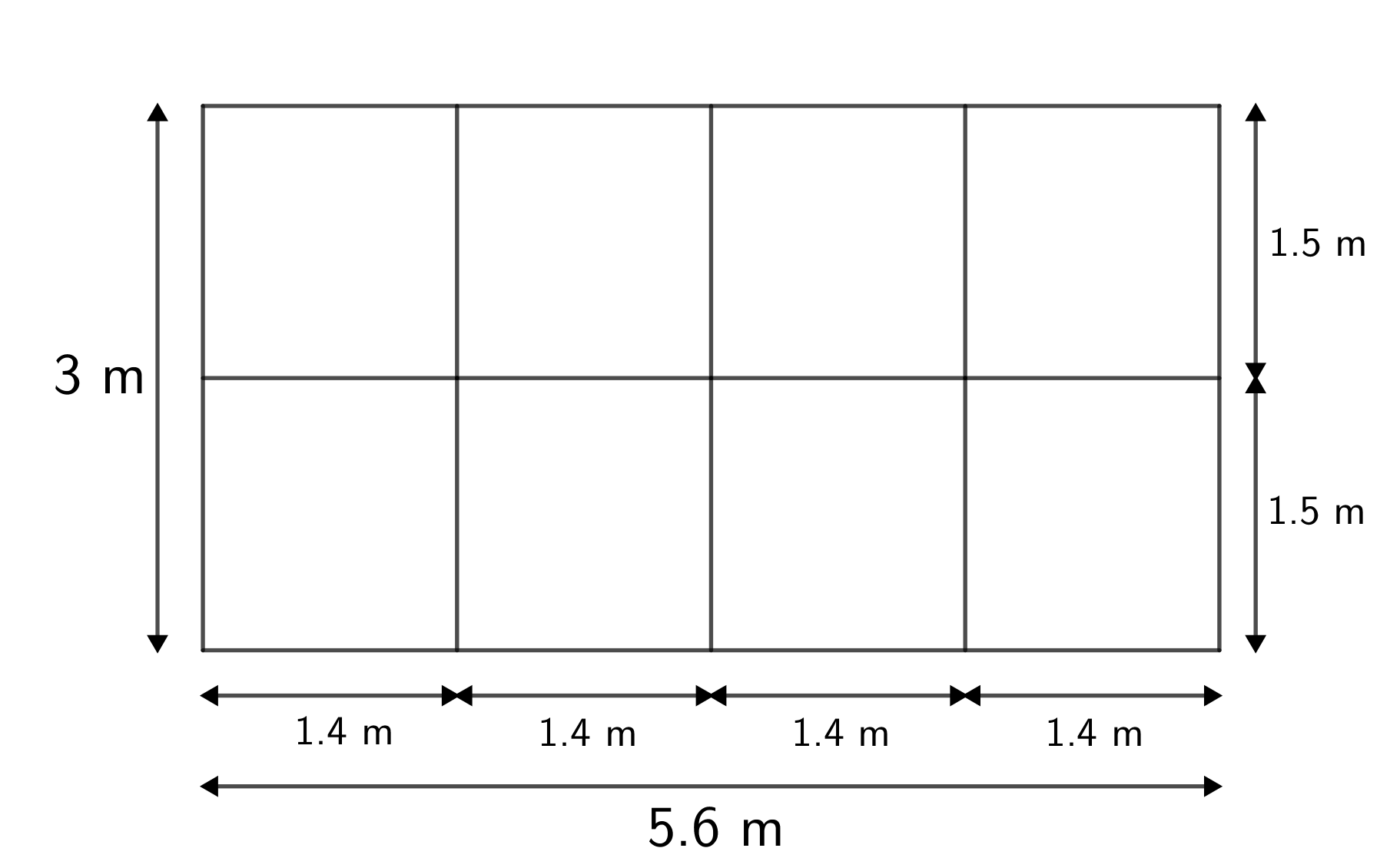
Her wagon deck is \(5.6\) m long and \(3\) m wide. Farmer Holly wants to tightly pack the hay bales on the wagon with the \(1.4\) m by \(1.5\) m side face down on the wagon. How many hay bales can she fit on her wagon if she does not stack them?

The total mass on the tires is equal to the mass of the hay plus the mass of the wagon. Since the wagon has four tires, the total mass the wagon can support is \(4\times 1100=4400\) kg. Subtracting the mass of the wagon, the total mass of hay the tires can support is \(4400 - 770=3630\) kg. If each hay bale weighs \(300\) kg, then the number of hay bales that could be supported is \(3630\div 300=12.1\) hay bales. Since there must be a whole number of hay bales, she could put \(12\) hay bales on her wagon without going over the maximum load.
Since \(5.6 =4\times 1.4\), and \(3= 2\times 1.5\), Farmer Holly could tightly pack \(4\times 2 = 8\) hay bales on her wagon in one layer.