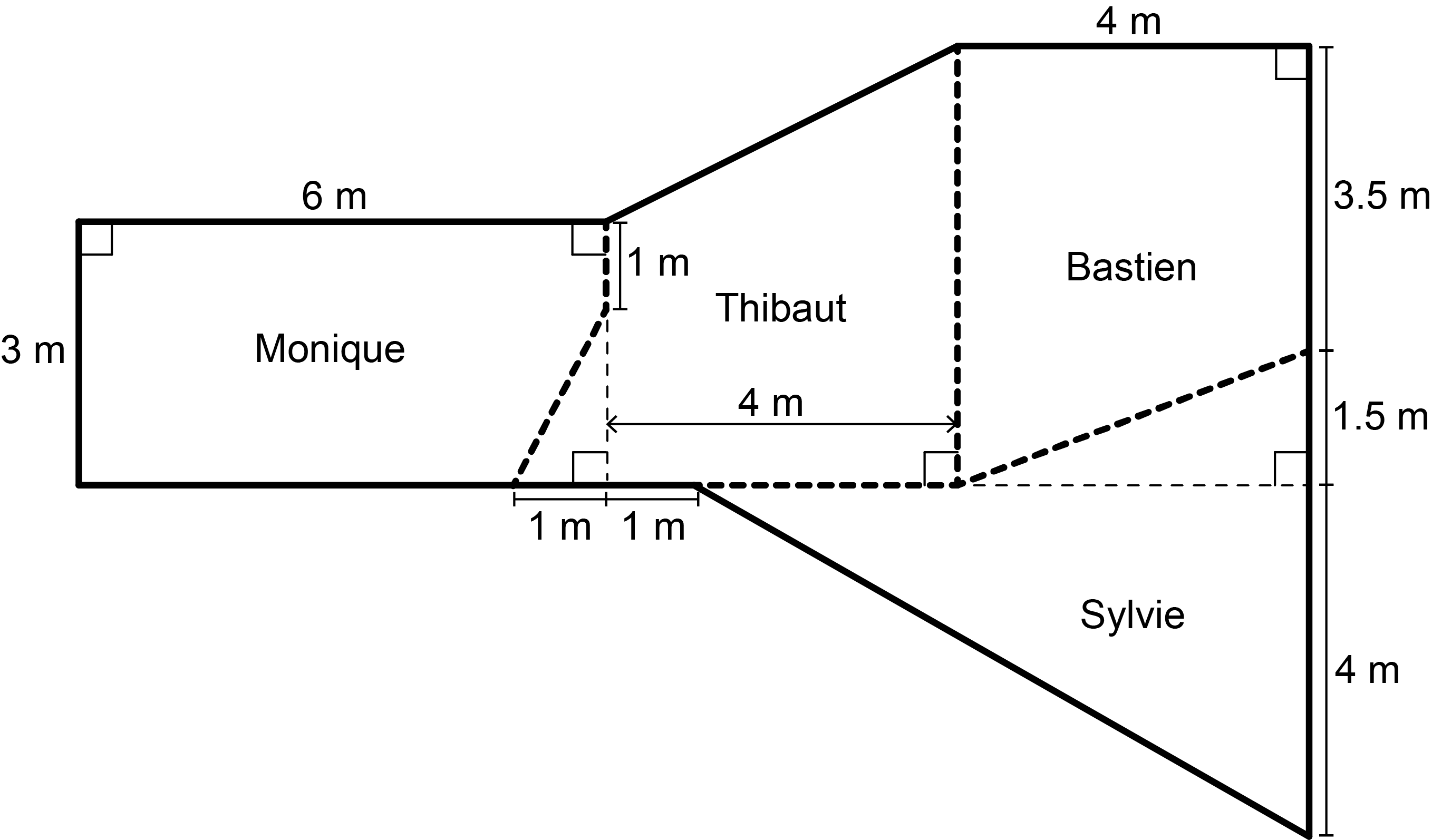

Monique, Thibaut, Bastien, and Sylvie are siblings who share an irregularly-shaped room in their home. They have divided up the room so that each person has their own space. Each person’s space is either a rectangle, a trapezoid, or a triangle. A floor plan, including some dimensions, is shown in the following diagram.

Calculate the area of each person’s space. Which person has the space with the largest area?
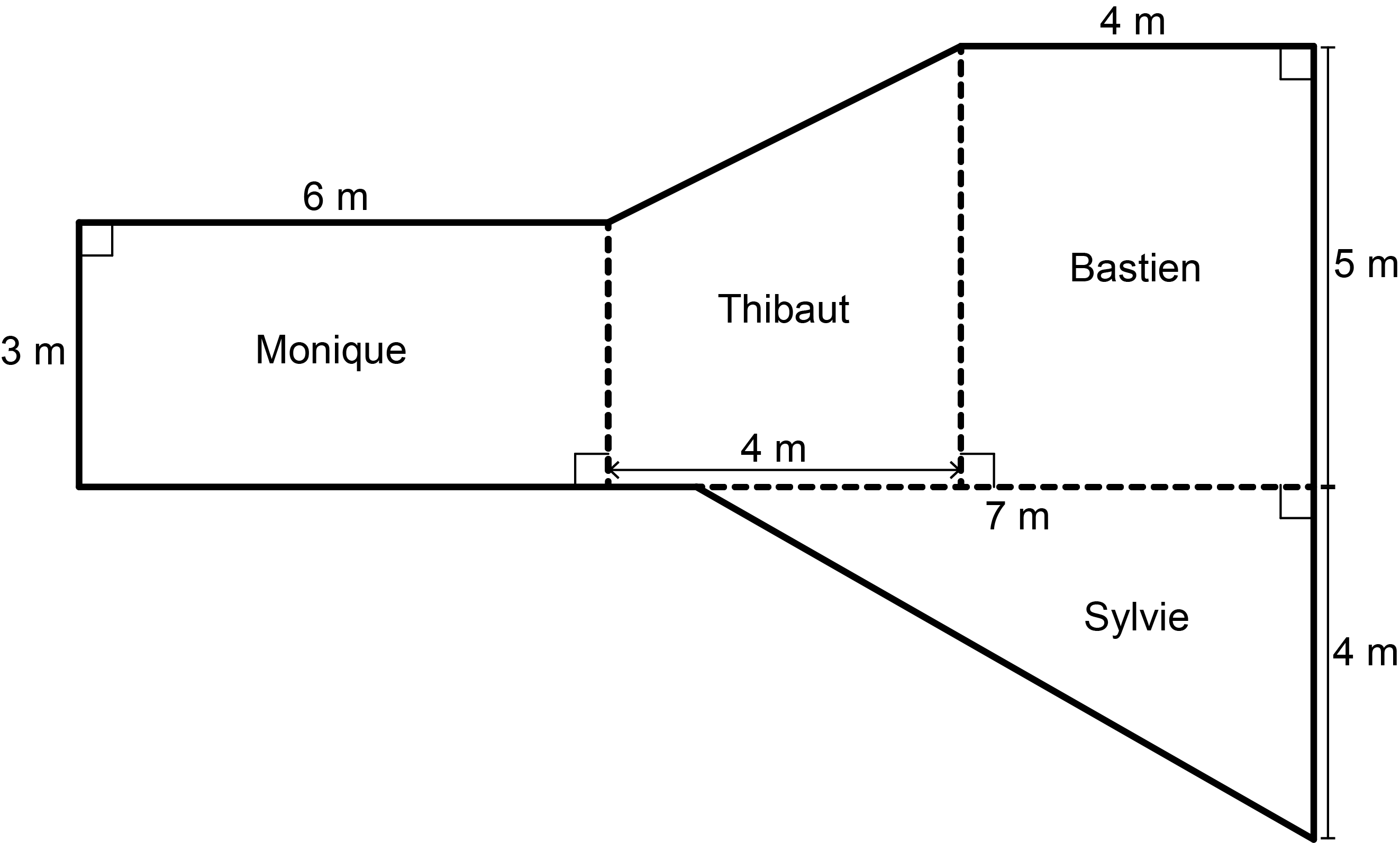
The siblings have decided to divide up the room in a different way so that the area of each person’s space is equal. After they do this, what is the area of each person’s space?
Redraw the inner dashed lines in the floor plan so that the area of each person’s space is equal. Note that the shape of each person’s space may no longer be a rectangle, trapezoid, or triangle.
Monique’s space is a rectangle with area \(6 \times 3 = 18~\text{m}^2\).
Thibaut’s space is a trapezoid with area \(\frac{1}{2} \times (3+5) \times 4=16~\text{m}^2\).
Bastien’s space is a rectangle with area \(4 \times 5 = 20~\text{m}^2\).
Sylvie’s space is a triangle with area \(\frac{1}{2} \times 7 \times 4 = 14~\text{m}^2\).
Thus, Bastien’s space has the largest area.
If the area of each person’s space is equal, then each person will have \(\frac{1}{4}\) of the area of the room. The area of the room is \(18+16+20+14=68~\text{m}^2\). Thus, the area of each person’s space will be \(\frac{1}{4} \times 68 = 17~\text{m}^2\).
There are many ways to redraw the inner lines so that each person’s space has an area of \(17~\text{m}^2\). It’s easiest if we first think about how each person’s space needs to change. Monique’s space currently has an area of \(18~\text{m}^2\), so we need to remove an area of \(1~\text{m}^2\). Thibaut’s space currently has an area of \(16~\text{m}^2\), so we need to add an area of \(1~\text{m}^2\). Bastien’s space currently has an area of \(20~\text{m}^2\), so we need to remove an area of \(3~\text{m}^2\). Sylvie’s space currently has an area of \(14~\text{m}^2\), so we need to add an area of \(3~\text{m}^2\).
One way to do this is to take a square \(1~\text{m}^2\) area from Monique’s space and give it to Thibaut, and then take a rectangular \(3~\text{m}^2\) area from Bastien’s space and give it to Sylvie. To achieve this, we can redraw two of the inner dashed lines as shown in the following floor plan.
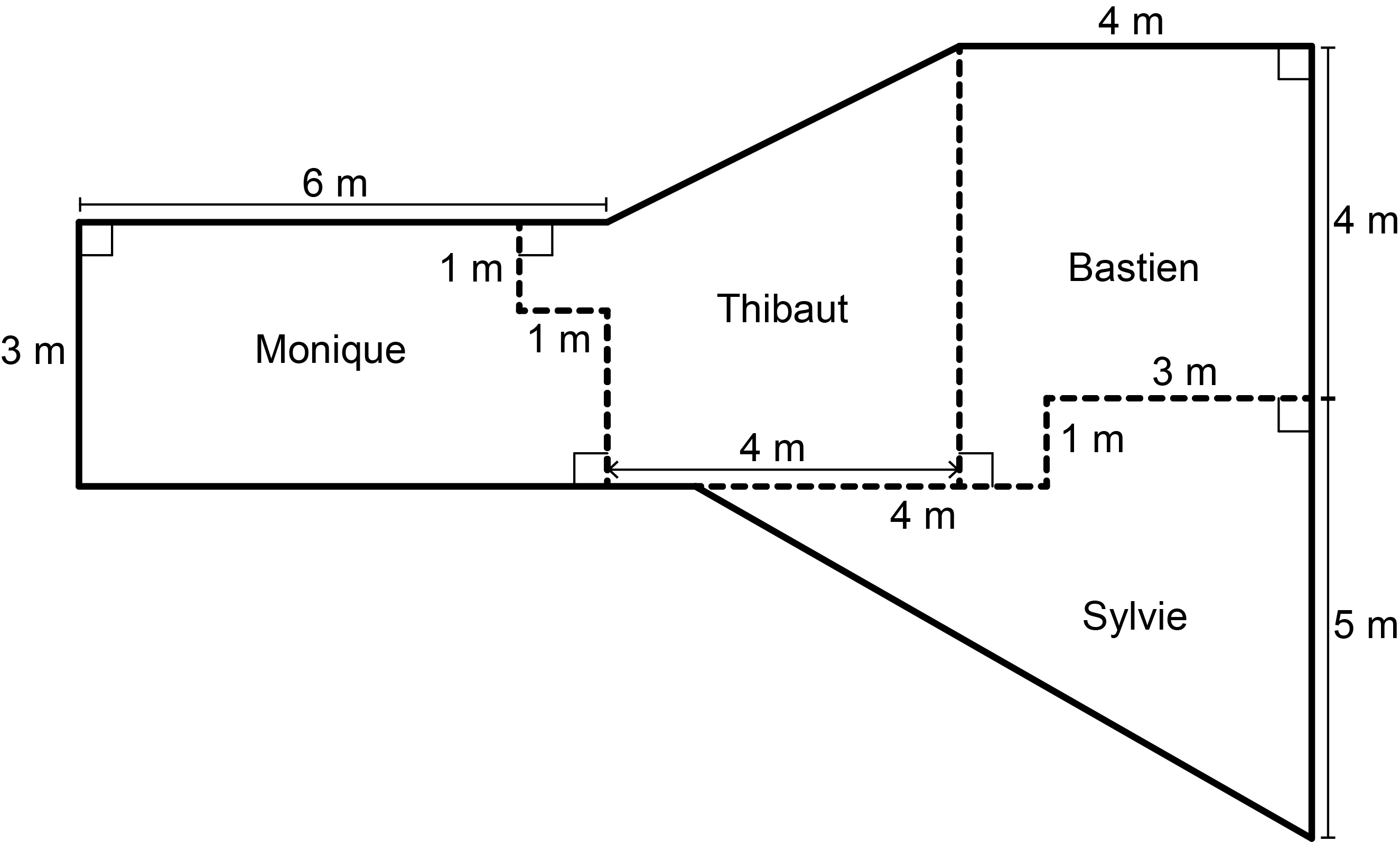
Alternatively, we could reassign triangular areas instead of rectangular areas. One way to do this is shown in the following floor plan.