Solution

Problem

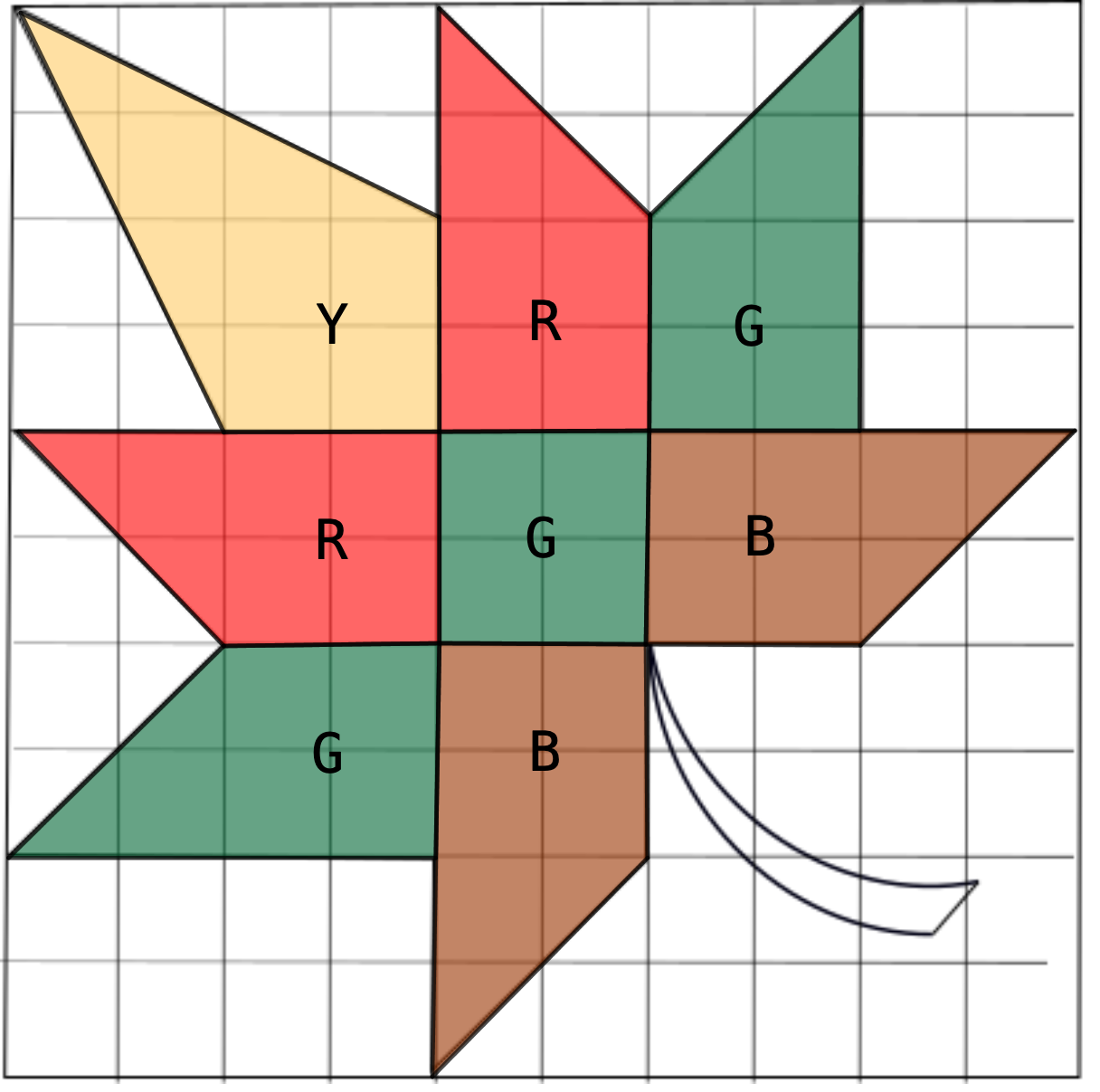
The \(10\,\)cm by \(10\,\)cm square on the left is the pattern for a single square in the maple leaf quilt on the right. In the pattern, the interior of the maple leaf has been divided into eight shapes, which have each been coloured yellow (Y), red (R), green (G), or brown (B). The rest of the square, including the stem, is white.

A 10 by 10 grid with the outline of a maple leaf drawn on the grid. The top point of the leaf is in one corner of the grid and each of the other six points of the leaf is touching an edge of the grid. The maple leaf covers a large portion of the area of the grid.

Straight line segments divide the interior of the maple leaf into eight pieces. The pieces are coloured using four different colours. A description of the colours and shapes of the pieces follows.

One four sided yellow shape with one right angle forms the middle point of the leaf. The shape lies inside a 4 by 4 square on the grid. The four vertices are placed as follows: top left corner of the square, midpoint of the right side of the square, bottom right corner of the square, and midpoint of the bottom side of the square.
Two red trapezoids, two green trapezoids, and two brown trapezoids form the six points of the leaf with one of each colour on each side of the leaf. Each trapezoid has the same shape and size. The parallel sides are of length 4 and 2. One of the remaining sides is of length 2 and meets both parallel sides at a right angle.
One green square with side length 2 is at the centre of the leaf.

Draw dotted lines on the pattern which divide the interior of each coloured shape into pieces that are squares or triangles.

For each of the four colours in the pattern, what is the area of the maple leaf that is covered by that colour?

What is the area of the rest of the pattern, including the stem, that is white? That is, what is the area of the square that is not covered by the leaf?

Solution

One way to divide the interior of each coloured shape into pieces that are squares or triangles has been shown below.

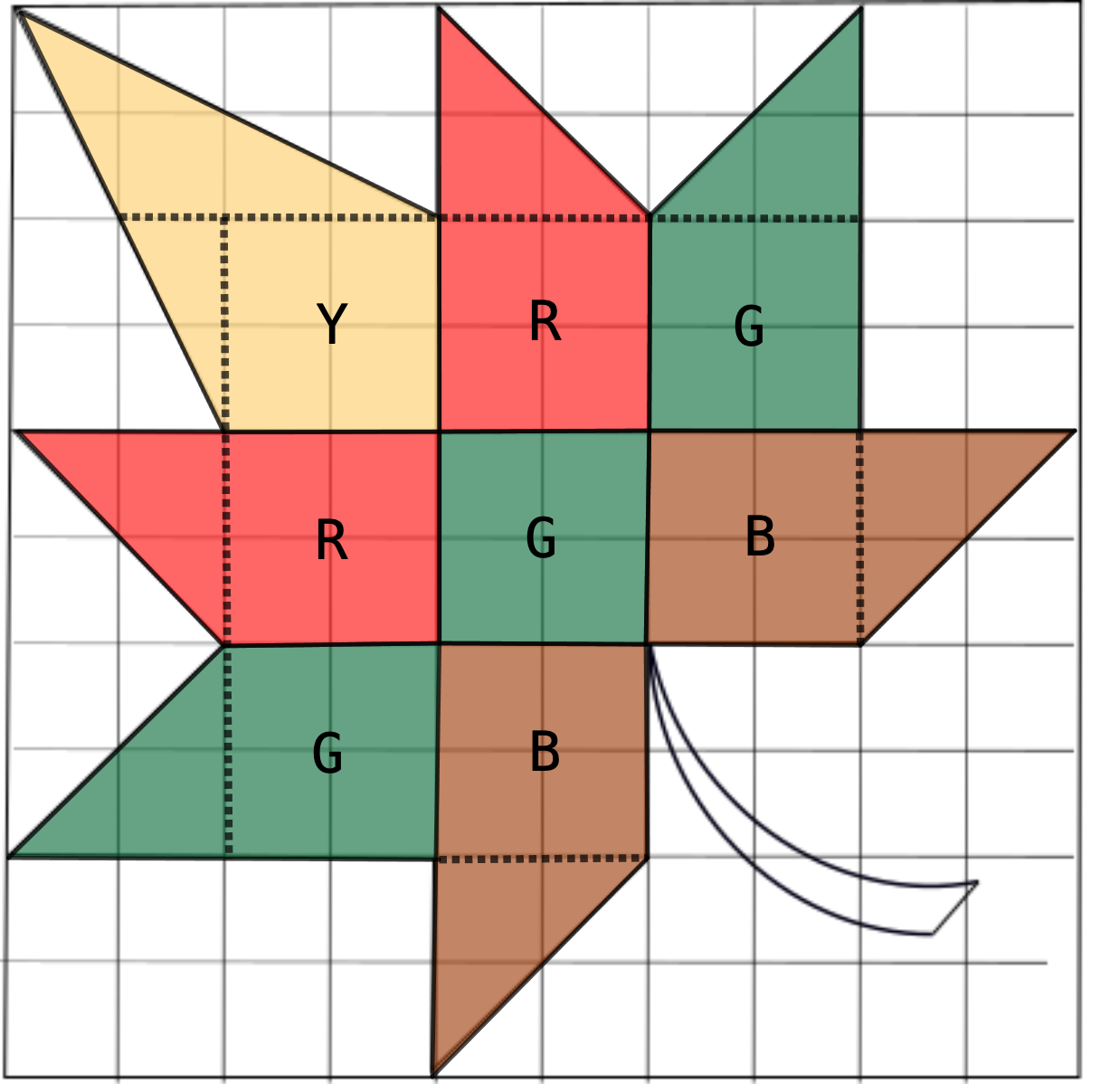
The two red regions each consist of a square with area \(2 \times 2 = 4 \,\text{cm}^2\) and a triangle with area \(2 \times 2 \div 2 = 2\, \text{cm}^2\). Therefore, the area of one red region is \(4+ 2= 6\,\text{cm}^2\), and the total area of the two red regions is \(2 \times 6 = 12 \,\text{cm}^2\).

The two brown regions also each consist of a square with area \(2 \times 2 = 4 \,\text{cm}^2\) and a triangle with area \(2 \times 2 \div 2 = 2\, \text{cm}^2\). Therefore, the area of one brown region is \(4+ 2= 6\,\text{cm}^2\), and the total area of the two brown regions is \(2\times 6 = 12\,\text{cm}^2\).

The three green regions consist of two shapes that have the same dimensions as the red shapes, and the centre square. Since the area of the centre square is \(2\times 2 = 4\,\text{cm}^2\), the area of the three green regions is \(12+4=16\,\text{cm}^2\).

The yellow region has an area equal to the area of the \(4\,\)cm by \(4\,\)cm square in the upper left corner minus the areas of the two white triangles in that square. Each of these triangles has a base of \(2\,\)cm and a height of \(4\,\)cm, and so has an area of \(2\times 4 \div 2=4\,\text{cm}^2\). Therefore, the total area of the white triangles is \(4 + 4 = 8\,\text{cm}^2\). Thus, the area of the yellow region is \(4\times 4 - 8 =16-8=8\,\text{cm}^2\).

The total area of the maple leaf, excluding the stem, is the sum of the areas of the red, brown, green, and yellow coloured regions, or \(12+12+16+8=48\,\text{cm}^2\).

Thus, the area of square that is not covered by the leaf is equal to the total area of the square minus the total coloured area or \(10\times 10 - 48 = 52\,\text{cm}^2\).

Problem of the Week Problem B and Solution Maple Leaf Quilting

Problem

Solution

Problem of the Week
Problem B and Solution
Maple Leaf Quilting