
Consider pentagon \(PQRST\). Starting at \(P\) and moving around the pentagon, the vertices are labelled \(P\), \(Q\), \(R\), \(S\), and \(T\), in order.
The pentagon has right angles at \(P\), \(Q\), and \(R\), obtuse angles at \(S\) and \(T\), and an area of \(1000\mbox{ cm}^2\).
Point \(V\) lies inside the pentagon such that \(\angle PTV\), \(\angle TVS\), and \(\angle VSR\) are right angles.
Point \(U\) lies on \(TV\) such that \(\triangle STU\) has an area of \(210\mbox{ cm}^2\). Also, it is known that \(PQ=50\) cm, \(SR=15\) cm, and \(TU=30\) cm.
Determine the length of \(PT\).

Extend \(TV\) to meet \(QR\) at \(W\). We mark this and all of the given information on the diagram.
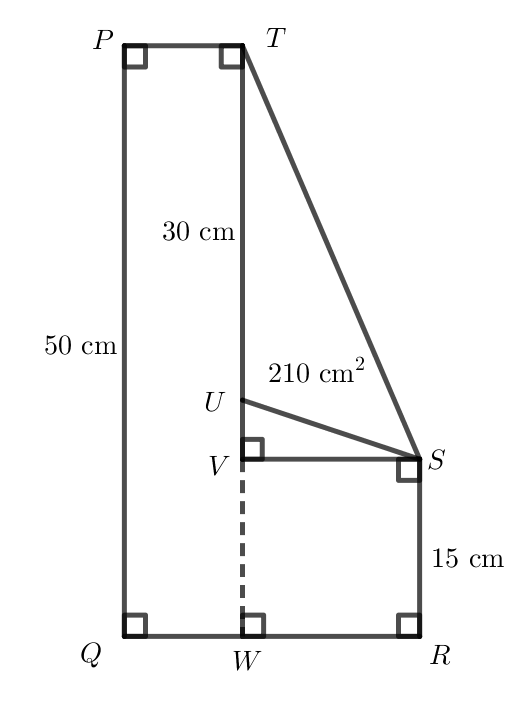
To find the area of a triangle, multiply the length of the base by the height and divide by 2. In \(\triangle STU\), the base \(TU\) has length \(30\) cm. The corresponding height of \(\triangle STU\) is the perpendicular distance from \(TU\) (extended) to vertex \(S\), namely \(SV\).
Since the area of \(\triangle STU\) is given to be \(210\) cm\(^2\), \[\begin{aligned} 210 &=\frac{30\times SV}{2}\\ 210&=15\times SV\\ 14&=SV\end{aligned}\]
We know that \(TW=PQ=50\), \(VW=SR=15\), and \(TW = TU+UV+VW\).
It follows that \(50=30+UV+15\) and \(UV=5\) cm.
Now we can relate the total area of the pentagon to the areas of the shapes inside. \[\begin{aligned} \text{Area }PQRST&=\text{Area }PQWT+\text{Area }RSVW+\text{Area }\triangle SUV+\text{Area }\triangle STU\\ 1000&=PQ\times PT+SV\times SR+\frac{UV\times SV}{2}+210\\ 1000&=50\times PT+14\times 15+\frac{5\times 14}{2}+210\\ 1000&=50\times PT+210+35+210\\ 1000&=50\times PT+455\\ 1000-455&=50\times PT\\ 545&=50\times PT\\ \frac{545}{50}&=PT\end{aligned}\] Therefore, \(PT=10.9\) cm.