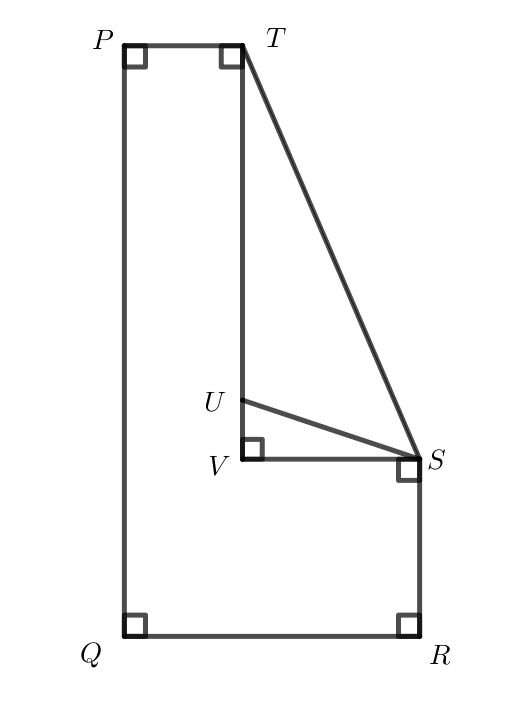

Consider pentagon \(PQRST\). Starting at \(P\) and moving around the pentagon, the vertices are labelled \(P\), \(Q\), \(R\), \(S\), and \(T\), in order.
The pentagon has right angles at \(P\), \(Q\), and \(R\), obtuse angles at \(S\) and \(T\), and an area of \(1000\mbox{ cm}^2\).
Point \(V\) lies inside the pentagon such that \(\angle PTV\), \(\angle TVS\), and \(\angle VSR\) are right angles.
Point \(U\) lies on \(TV\) such that \(\triangle STU\) has an area of \(210\mbox{ cm}^2\). Also, it is known that \(PQ=50\) cm, \(SR=15\) cm, and \(TU=30\) cm.
Determine the length of \(PT\).

Themes: Algebra, Geometry