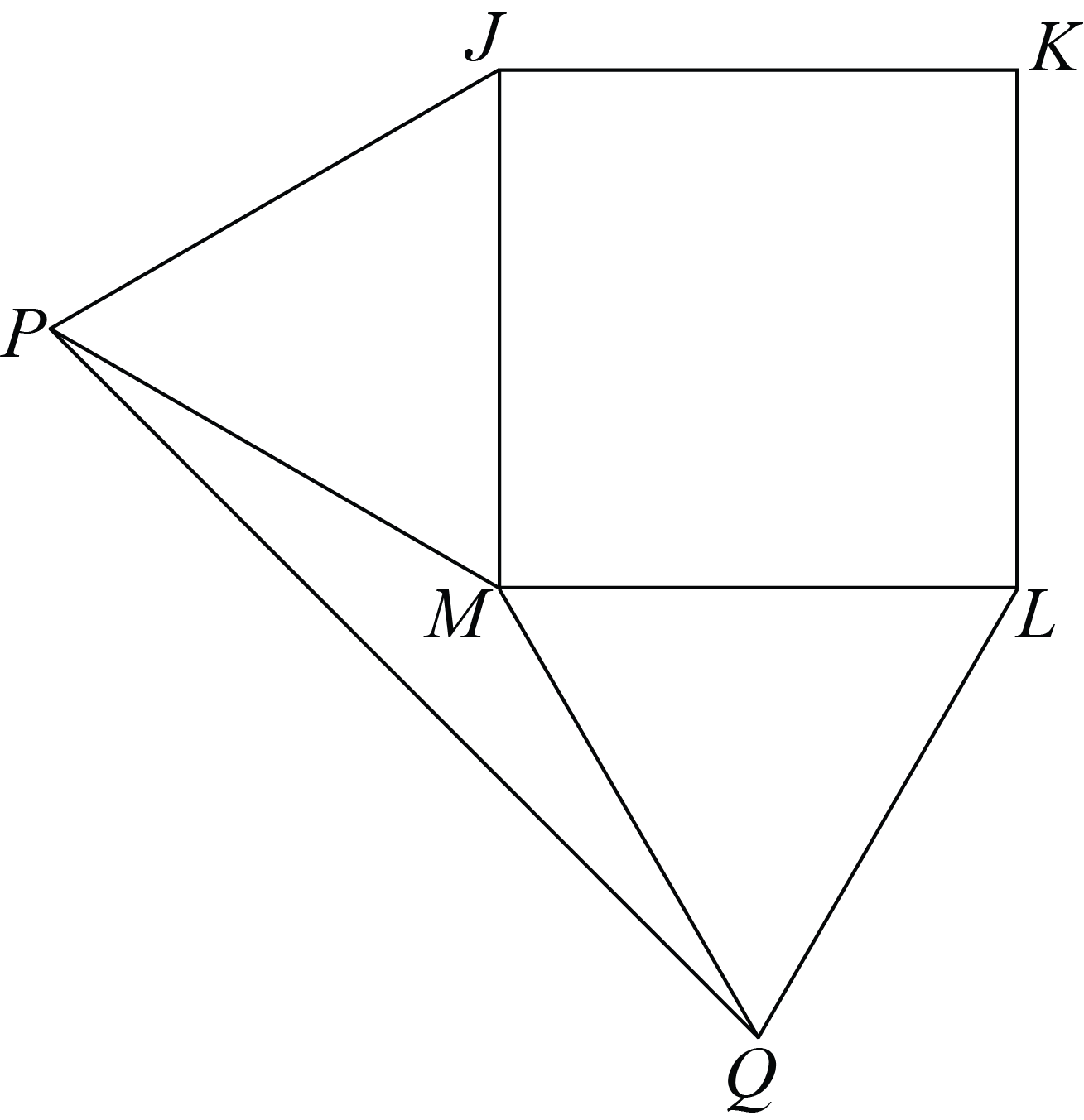

Ziibi drew a square. Starting at one corner and moving around the square, he labelled the vertices \(J\), \(K\), \(L\), and \(M\), in order. He drew points \(P\) and \(Q\) outside the square so that both \(\triangle JMP\) and \(\triangle MLQ\) are equilateral.

Determine the measure, in degrees, of \(\angle MPQ\).
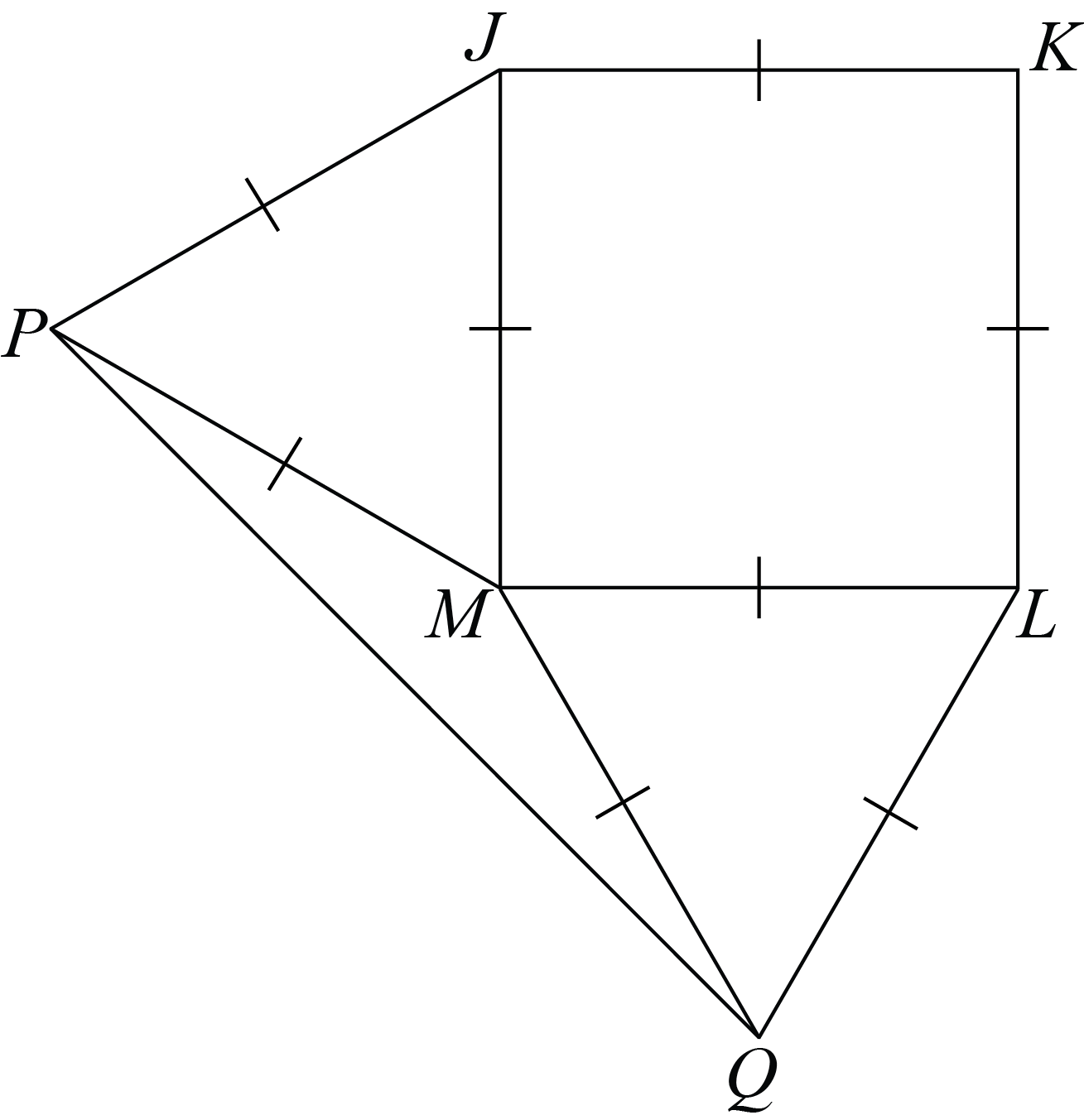
Since \(JKLM\) is a square, \(JK=KL=LM=MJ\).
Since \(\triangle JMP\) is equilateral, \(MJ=JP=MP\).
Since \(\triangle MLQ\) is equilateral, \(LM=LQ=QM\).
It follows that \[JK=KL=LM=MJ=JP=MP=LQ=QM.\]
Each angle in a square is \(90^{\circ}\). Therefore, \(\angle JML =90^{\circ}\).
Each angle in an equilateral triangle is \(60^{\circ}\). Therefore, \(\angle JMP =60^{\circ}\) and \(\angle LMQ =60^{\circ}\).
A complete revolution is \(360^{\circ}\). Since \(\angle PMQ\), \(\angle JMP\), \(\angle JML\), and \(\angle LMQ\) form a complete revolution, then \[\begin{aligned} \angle PMQ&=360^\circ -\angle JMP-\angle JML-\angle LMQ\\ &=360^\circ - 60^\circ -90^\circ-60^\circ\\ &=150^\circ\end{aligned}\]
In \(\triangle MPQ\), \(MP=QM\) and the triangle is isosceles. It follows that \(\angle MPQ=\angle MQP\).
In a triangle, the sum of the three angles is \(180^\circ\). Since \(\angle PMQ=150^\circ\), then the sum of the two remaining equal angles must be \(30^\circ\). Therefore, each of the remaining two angles must equal \(15^\circ\) and it follows that \(\angle MPQ=15^\circ\).