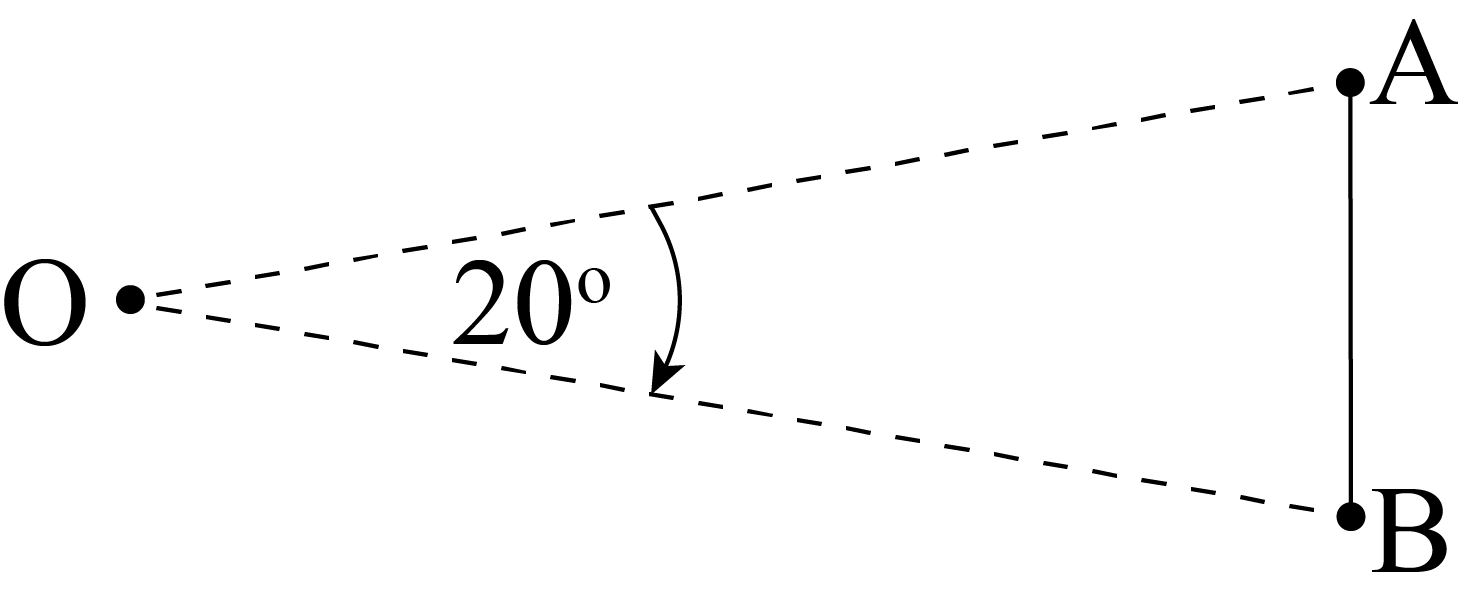

Priya is drawing a polygon on a piece of wood. First she hammers a nail into the piece of wood, calling this point \(O\). Then she attaches one end of a piece of string to the nail, and the other end to a pencil. She pulls the string tight and makes a dot on the wood, calling this point \(A\). Keeping the string tight, she rotates it \(20^\circ\) clockwise and makes another dot, calling this point \(B\). She then connects points \(A\) and \(B\) with a straight line.

She repeats this process, rotating the string \(20^\circ\) clockwise, making a dot, and connecting this point to the previous point with a straight line each time, until she has gone all the way around the circle and completed the polygon.

How many sides does Priya’s completed polygon have?
What is the sum of all the interior angles in the polygon?
Each time the process is repeated, another congruent triangle is created. Each of these triangles has a \(20^\circ\) angle at \(O\), the centre of the circle. Since a complete rotation at the centre is \(360^\circ\), that means there are \(360\div 20=18\) triangles formed. Since each triangle has one edge on the side of the polygon, it follows that the polygon has \(18\) sides. An \(18\)-sided polygon is called an octadecagon, from octa meaning \(8\) and deca meaning \(10\).
Since the distance between each dot and point \(O\) (the nail) is always the same, it follows that the two sides of each congruent triangle that connect to point \(O\) are equal. Therefore, the congruent triangles are all isosceles, and the angles that are not at point \(O\) are all equal. The angles in a triangle sum to \(180^\circ\), so after the \(20^\circ\) angle is removed, there is \(160^\circ\) remaining for the other two angles. It follows that each of the other two angles in each triangle measures \(160^\circ \div 2=80^\circ\). The following diagram illustrates this information for the two adjacent triangles \(AOB\) and \(BOC\).
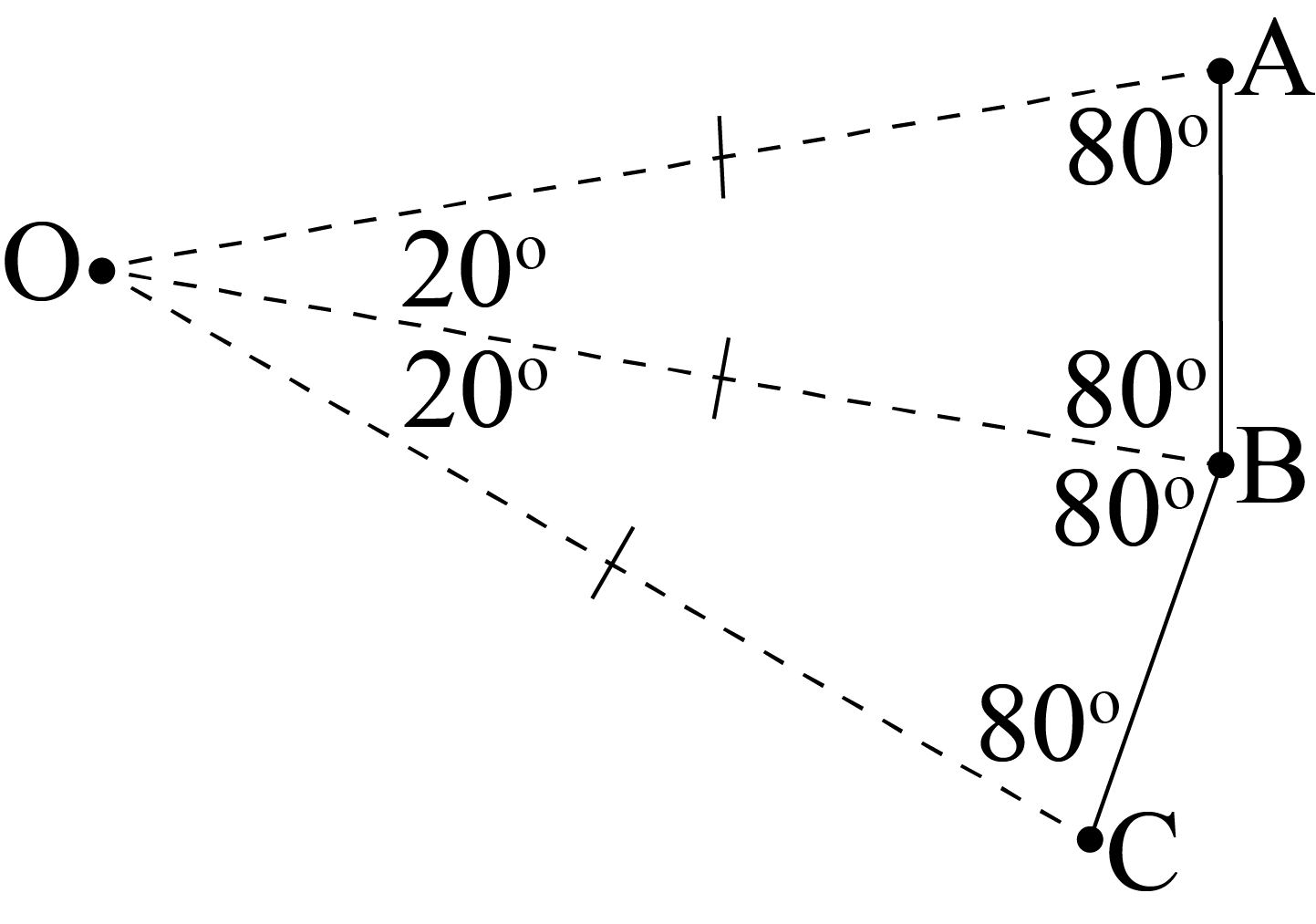
Each interior angle in the polygon is formed by an \(80^\circ\) angle from one triangle and the adjacent \(80^\circ\) angle from the next triangle. It follows that each interior angle measures \(80^\circ+80^\circ=160^\circ\). Thus, there are \(18\) interior angles in the octadecagon and each angle measures \(160^\circ\).
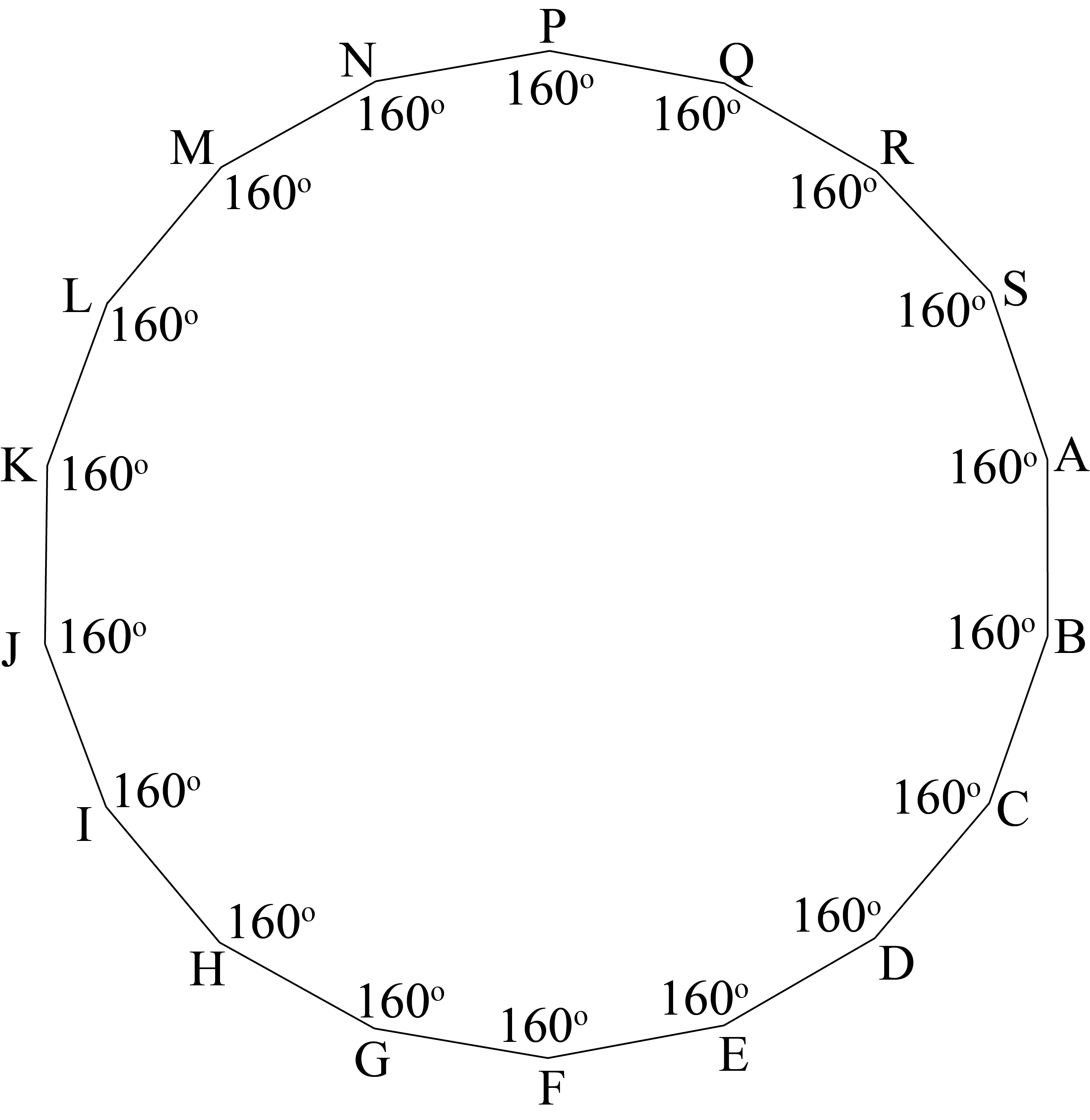
Therefore, the sum of all the interior angles in the octadecagon is \(18\times 160^\circ=2880^\circ\).