

Tesfaye built a robot that can paint a path as it moves around a piece of paper. The robot uses the Cartesian coordinate system and starts on the point \((0,0)\). Users enter a list of points and the robot moves from one point to the next point in the list in a straight line, painting the path it travels. After it reaches the last point, it goes back to the point \((0,0)\).
Tesfaye entered the following coordinates into the robot: \[(1,1),~ (-1,3),~ (-3,3),~ (-3,1),~\text{and}~ (-2,-2).\] Calculate the area of the shape that the robot painted.

Extension: What is the total distance traveled by the robot?
Note: You may find the following useful for the extension:
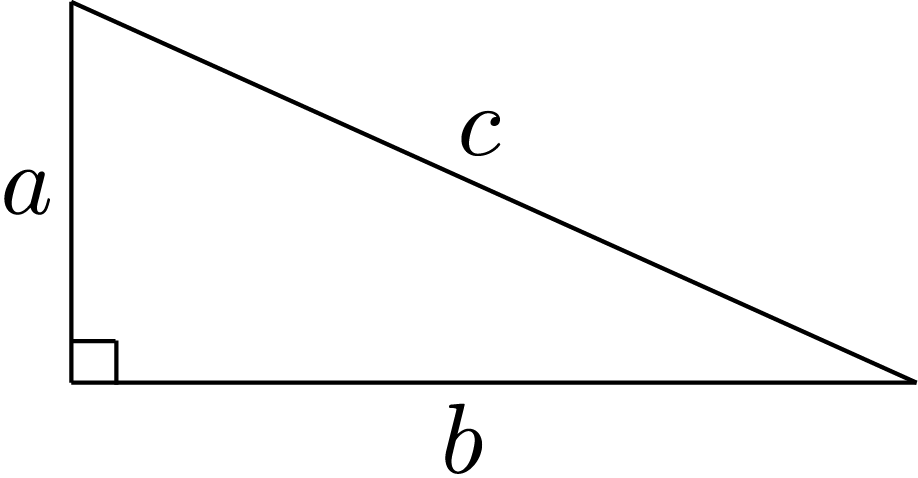
The Pythagorean Theorem states, “In a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) equals the sum of the squares of the lengths of the other two sides.”
In the right-angled triangle shown, \(c\) is the hypotenuse, \(a\) and \(b\) are the lengths of the other two sides, and \(c^2=a^2+b^2\).
Theme: Geometry