

Tesfaye built a robot that can paint a path as it moves around a piece of paper. The robot uses the Cartesian coordinate system and starts on the point \((0,0)\). Users enter a list of points and the robot moves from one point to the next point in the list in a straight line, painting the path it travels. After it reaches the last point, it goes back to the point \((0,0)\).
Tesfaye entered the following coordinates into the robot: \[(1,1),~ (-1,3),~ (-3,3),~ (-3,1),~\text{and}~ (-2,-2).\] Calculate the area of the shape that the robot painted.

Extension: What is the total distance traveled by the robot?
Note: You may find the following useful for the extension:
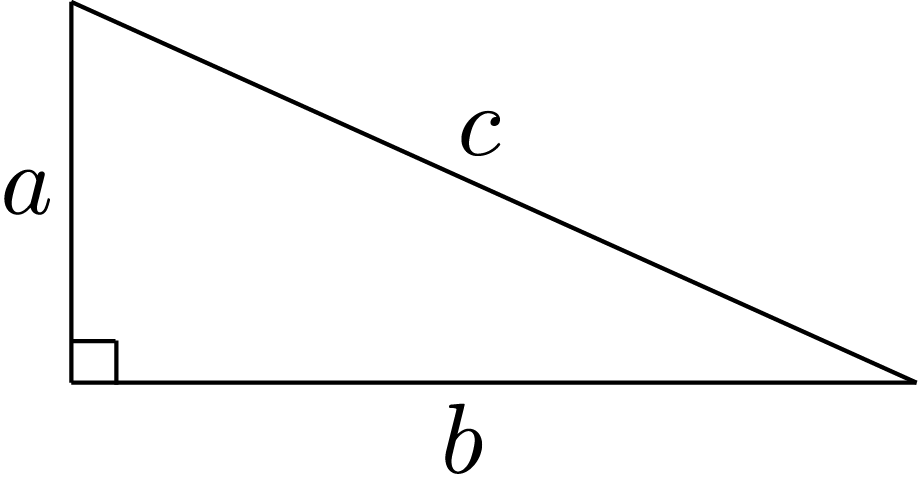
The Pythagorean Theorem states, “In a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) equals the sum of the squares of the lengths of the other two sides.”
In the right-angled triangle shown, \(c\) is the hypotenuse, \(a\) and \(b\) are the lengths of the other two sides, and \(c^2=a^2+b^2\).
First we will draw the shape that the robot painted. We label the points \(A(0,0),~B(1,1),~C(-1,3),~D(-3,3),~E(-3,1),\) and \(F(-2,-2)\) on the Cartesian plane and connect the points forming polygon \(ABCDEF\).

We will make a note here about points \(F,~A,\) and \(B\). If we move \(1\) unit right and \(1\) unit up from \(F(-2,-2),\) we get to \((-1,-1)\). If we move \(1\) unit right and \(1\) unit up from \((-1,-1),\) we get to \(A(0,0)\). If we move \(1\) unit right and \(1\) unit up from \(A(0,0),\) we get to \(B(1,1)\). This illustrates that the points \(F,~A,\) and \(B\) lie on the same line. A detailed discussion of this is provided in high school math courses.
From here, we will present two solutions.
Solution 1
In Solution \(1\), we will solve the problem by dividing the shape into smaller, more familiar shapes.
There are several ways to do this. One way is to add point \(G(-1,1)\) on line segment \(EB\) and notice that segments \(EB\) and \(CG\) divide the shape into square \(CDEG\), \(\triangle BCG\), and \(\triangle BEF\) as shown.

Point \(H(-2,1)\) on \(EB\) is also added to form altitude \(FH\) of \(\triangle BEF\).
We will now calculate the area of each shape and then add these together to find the total area of the shape that the robot painted.
\[\begin{aligned} \text{area of square }CDEG &=CD \times DE\\ &=2\times 2\\ &=4~\text{units}^2\end{aligned}\] \[\begin{aligned} \text{area of }\triangle BCG &=\frac{1}{2} \times BG \times CG\\ &=\frac{1}{2} \times 2\times 2\\ &=2~\text{units}^2\end{aligned}\] \[\begin{aligned} \text{area of }\triangle BEF &=\frac{1}{2} \times BE \times FH\\ &=\frac{1}{2} \times 4\times 3\\ &=6~\text{units}^2\end{aligned}\]
Therefore, the total area of \(ABCDEF\) is \(4+2+6=12~\text{units}^2\).
Note that if we had not used the information that the points \(F,~A,\) and \(B\) are on the same line, then we would have had to further break up the region \(BEF\) into triangles and trapezoids to calculate the area.
Solution 2
In Solution \(2\), we will solve the problem by putting the shape inside a rectangle.
One way to do this is to add the points \(G(-3,-2),~H(1,-2),\) and \(I(1,3)\) and notice that \(DGHI\) is a rectangle that contains the shape \(ABCDEF\) painted by the robot. Also, the area of rectangle \(DGHI\) is covered exactly by shape \(ABCDEF\) and three right-angled triangles, \(\triangle EFG\), \(\triangle BFH\), and \(\triangle BCI\).

To calculate the area of \(ABCDEF\), we will subtract the areas of the three triangles from the area of the rectangle.
\[\begin{aligned} \text{area of rectangle }DGHI &=GH \times DG\\ &=4\times 5\\ &=20~\text{units}^2\end{aligned}\] \[\begin{aligned} \text{area of }\triangle EFG &=\frac{1}{2}\times FG \times EG\\ &=\frac{1}{2}\times 1\times 3\\ &=1.5~\text{units}^2\end{aligned}\] \[\begin{aligned} \text{area of } \triangle BFH &=\frac{1}{2}\times FH \times BH\\ &=\frac{1}{2}\times 3\times 3\\ &=4.5~\text{units}^2\end{aligned}\] \[\begin{aligned} \text{area of }\triangle BCI &=\frac{1}{2}\times BI \times CI\\ &=\frac{1}{2}\times 2\times 2\\ &=2~\text{units}^2\end{aligned}\]
Therefore, the total area of \(ABCDEF\) is \(20-1.5-4.5-2=12~\text{units}^2\).
Note that if we had not used the information that the points \(F,~A,\) and \(B\) are on the same line, then we would have had to break the region \(BFH\) into a triangle and a trapezoid or two triangles and a rectangle to calculate the area.
Solution to the Extension
We will use the diagram from Solution 2 to help us calculate the lengths of the sides of \(ABCDEF\).
In Solution 2, we added the points \(G(-3,-2),~H(1,-2),\) and \(I(1,3)\). Notice that \(DGHI\) is a rectangle that contains the shape \(ABCDEF\) painted by the robot. Also, the area of rectangle \(DGHI\) is covered exactly by shape \(ABCDEF\) and three right-angled triangles, \(\triangle EFG\), \(\triangle BFH\), and \(\triangle BCI\).

We can determine that \(CD=2\) units and \(DE=2\) units using the diagram or the coordinates of the points. Note that the other three sides of \(ABCDEF\) are each the hypotenuse of a right-angled triangle. To find the lengths of these three sides, we can use the Pythagorean Theorem.
In \(\triangle EFG\),
\[\begin{aligned} EF^2&=EG^2 + FG^2\\ &=3^2 + 1^2\\ &=9+1\\ &=10\end{aligned}\]
Thus, \(EF=\sqrt{10}\).
In \(\triangle BFH\),
\[\begin{aligned} BF^2&=FH^2 + BH^2\\ &=3^2 + 3^2\\ &=9+9\\ &=18\end{aligned}\]
Thus, \(BF=\sqrt{18}\).
In \(\triangle BCI\),
\[\begin{aligned} BC^2&=BI^2 + CI^2\\ &=2^2 + 2^2\\ &=4+4\\ &=8\end{aligned}\]
Thus, \(BC=\sqrt{8}\).
The total distance traveled by the robot is the sum of all the side lengths of \(ABCDEF\). \[\begin{aligned} BC+CD+DE+EF+BF&=\sqrt{8}+2+2+\sqrt{10}+\sqrt{18}\\ &=4+\sqrt{8}+\sqrt{10}+\sqrt{18}\\ &\approx 14.2~\text{units}\end{aligned}\]
Therefore, the total distance traveled by the robot is approximately \(14.2\) units.