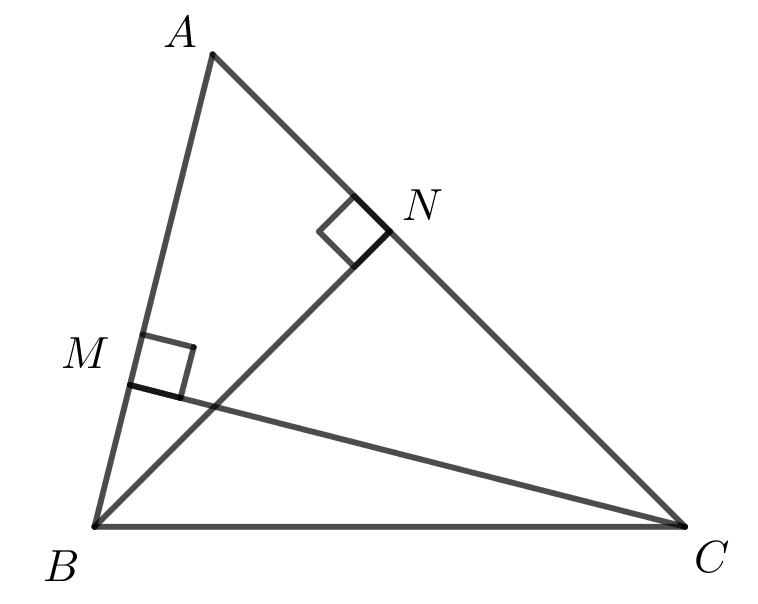

In acute \(\triangle ABC\), two altitudes have been drawn in. Point \(M\) lies on \(AB\) so that \(CM\) is an altitude of \(\triangle ABC\), and point \(N\) lies on \(AC\) so that \(BN\) is an altitude of \(\triangle ABC\).
Suppose \(CM=32\) cm, \(AB=36\) cm, and \(AC= 40\) cm. Determine the length of altitude \(BN\).

Note: An altitude of a triangle is the line segment drawn from a vertex of the triangle perpendicular to the opposite side.
The area of a triangle is determined using the formula \[\text{area} = \frac{\text{base} \times \text{height}}{2}\] The height of the triangle is the length of an altitude and the base of the triangle is the length of the side to which a particular altitude is drawn.
Thus, \[\begin{aligned} \text{Area } \triangle ABC&=\frac{AB\times CM}{2}\\ &=\frac{36\times 32}{2}\\ &=576\text{ cm}^2\end{aligned}\]
Also, \[\begin{aligned} \text{ Area } \triangle ABC&=\frac{AC\times BN}{2}\\ 576&=\frac{40\times BN}{2}\\ 1152&=40\times BN\\ BN&= 28.8 \text{ cm}\end{aligned}\]
Therefore, the length of altitude \(BN\) is \(28.8\) cm.