
A regular six-sided die has faces labelled with \(1, 2, 3, 4, 5\), and \(6\) dots. The number of dots on opposite faces add to seven. For example, the face with \(2\) dots is opposite the face with \(5\) dots.
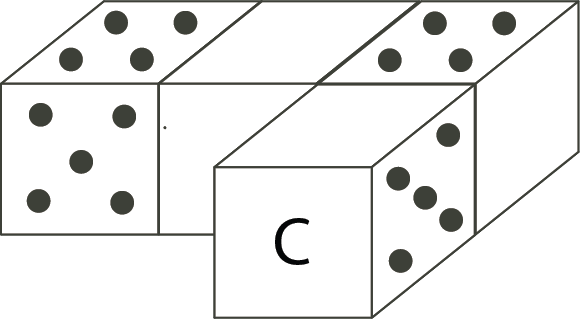
The four regular dice shown have been placed so that, for any two adjacent dice, the number of dots on the faces that are facing each other always add to nine. How many dots are on the face labelled \(C\)?

We will separate the four dice and refer to them as in the following diagram:
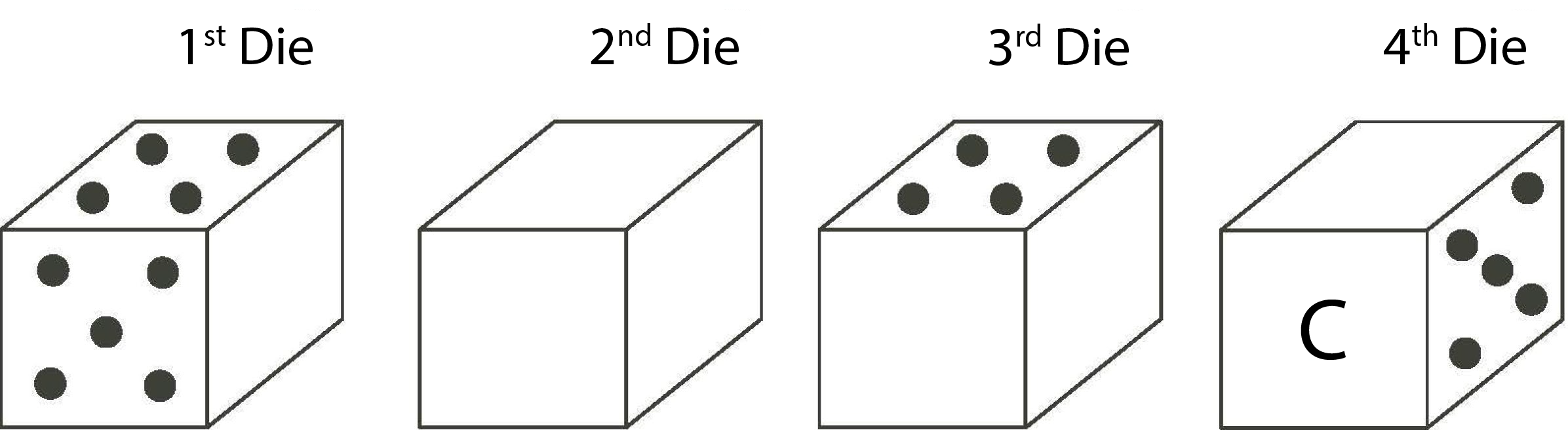
On the first die, since \(5\) dots are on the front, there are \(2\) dots on the back. Since \(4\) dots are on the top, there are \(3\) dots on the bottom. That leaves the faces with \(1\) and \(6\) dots for the sides. Since the number of dots on the sides facing each other add to \(9\), the right side of the first die must have \(6\) dots. If it were the face with \(1\) dot, the left face of the second die would have to have \(8\) dots, and that is not possible. Therefore, the right side of the first die must have \(6\) dots.
This means that the left side of the second die must have \(3\) dots, since number of dots on the sides facing each other add to \(9\). Since the left side of the second die has \(3\) dots, then the right side of the second die must have \(4\) dots, since the number of dots on opposite sides add to \(7\).
Then the left side of the third die must have \(5\) dots. If there are \(5\) dots on the left side, then there must be \(2\) dots on the right side. Since there are \(4\) dots on the top of the third die, there must be \(3\) dots on the bottom. That leaves \(1\) and \(6\) dots for the front and back of the third die. The front must have \(6\) dots in order for the number of dots on the front of the third die and the back of the fourth die to total to \(9\).
Since the front of the third die has \(6\) dots, the back of the fourth die must have \(3\) dots. If the back of the fourth die has \(3\) dots, then the front of the fourth die must have \(4\) dots. But the front of the fourth die is labelled \(C\). Therefore, there are \(4\) dots on the face labelled \(C\).