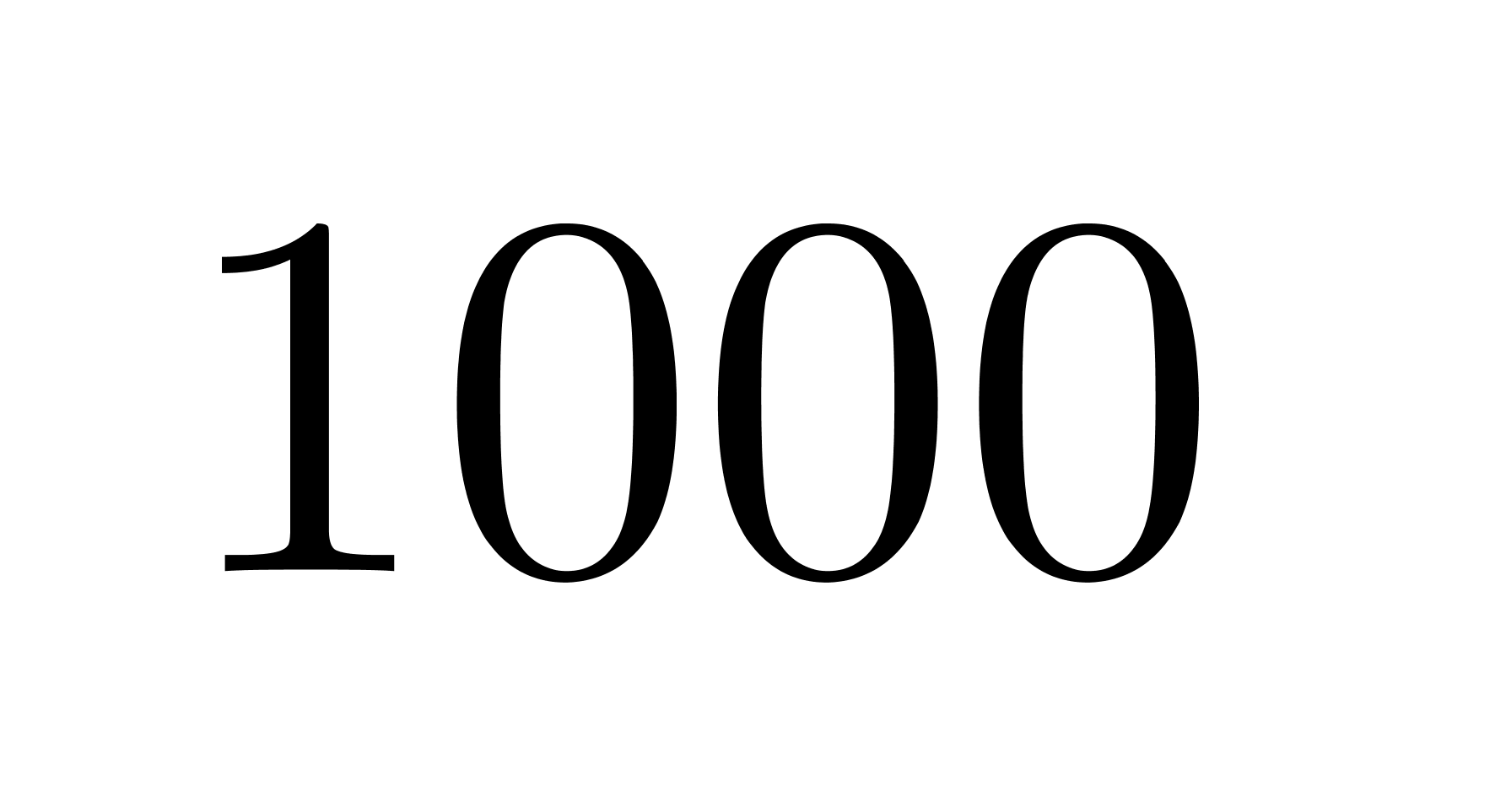

Did you know that \(1000\) can be written as the sum of the \(5\) consecutive positive integers beginning with \(198\)? That is, \[1000 = 198 + 199 + 200 + 201 + 202\]
Also, \(1000\) can be written as the sum of \(16\) consecutive positive integers beginning with \(55\). That is, \[1000 = 55+56+57+58+59+60+61+62+63+64+65+66+67+68+69+70\]
It is also possible to write \(1000\) as a sum of \(25\) consecutive positive integers. This is the maximum number of consecutive positive integers that could be used to create the sum. Determine the smallest of the positive integers in this sum.
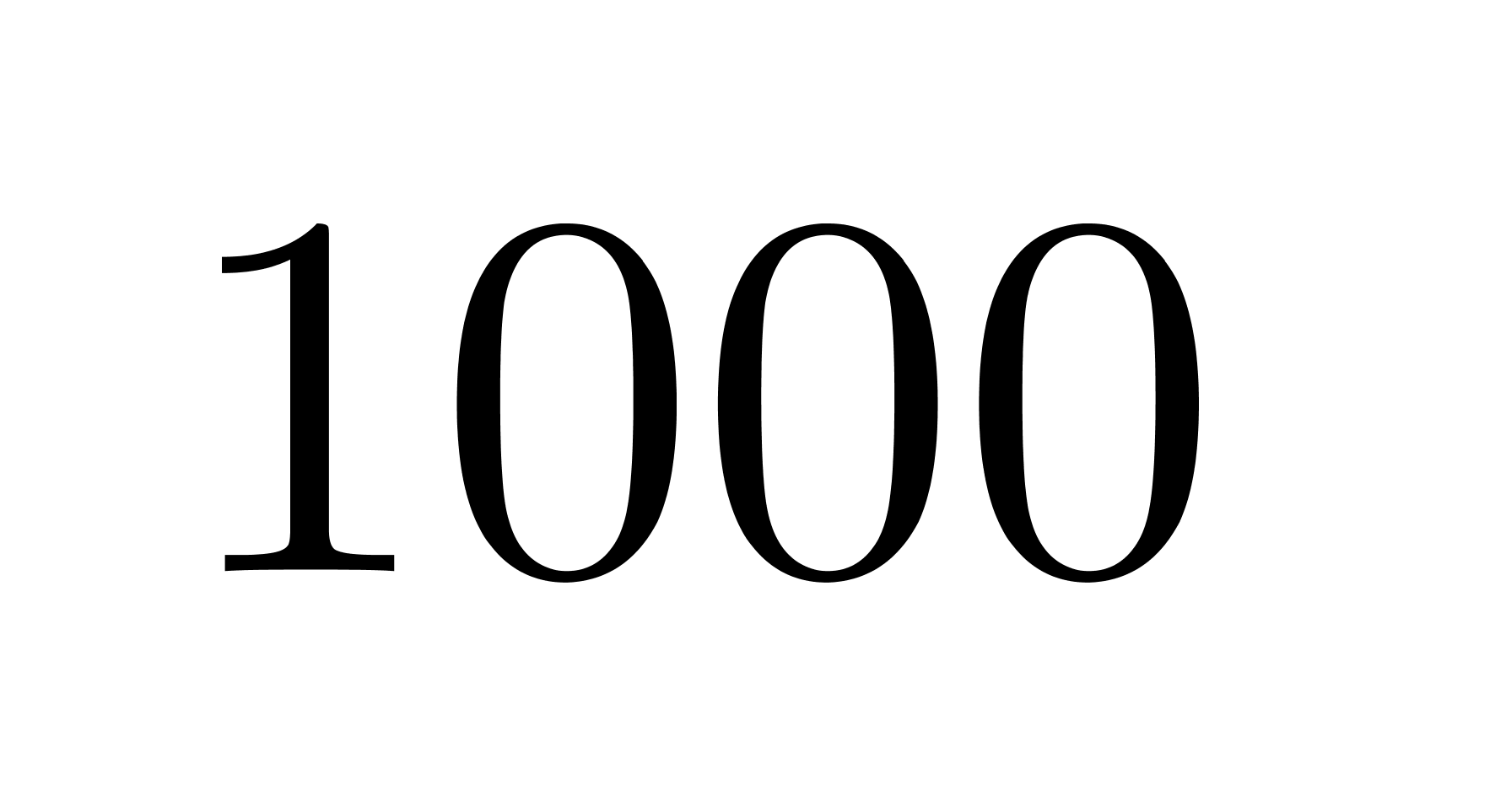
Theme: Number Sense