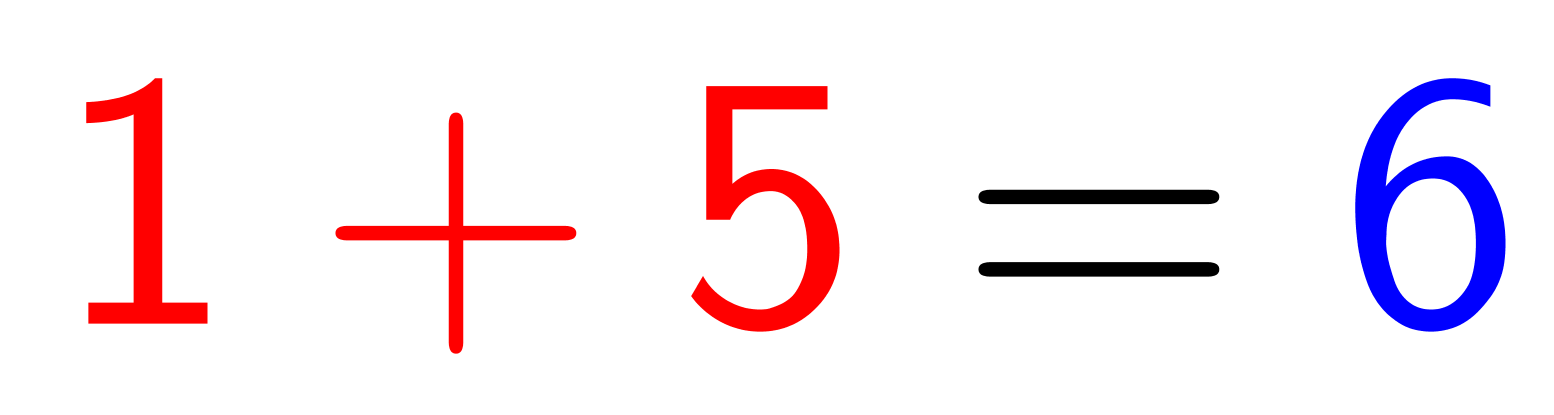

A \(3\)-digit positive integer is defined to be sumleft if the sum of its two leftmost digits is equal to its rightmost digit.
For example, the number \(156\) is sumleft since \(1+5 = 6\).
How many sumleft integers are there?
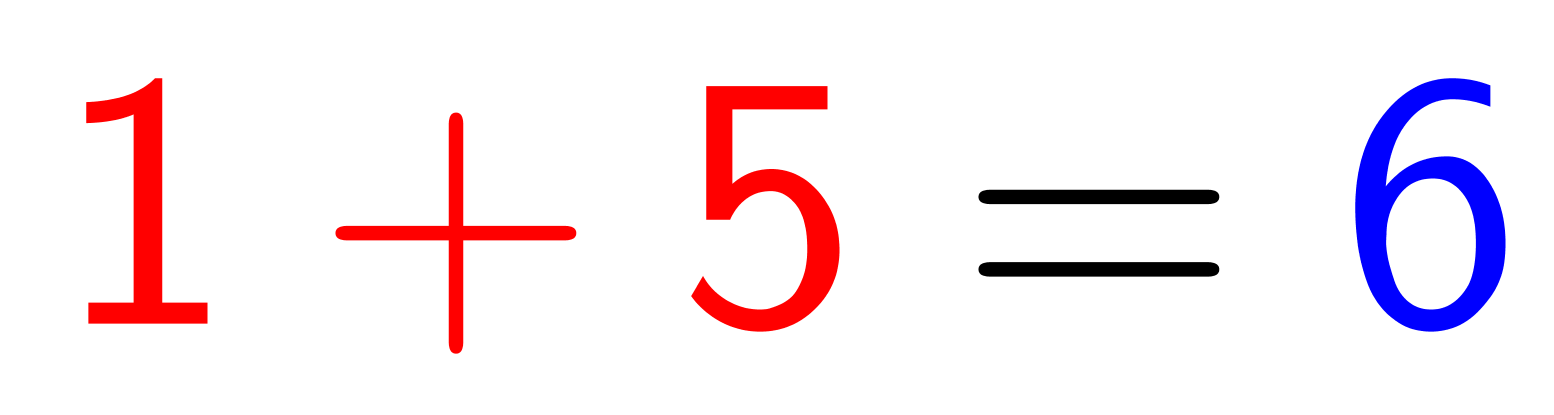
From the definition, the hundreds and tens digits of a sumleft integer will determine the ones (units) digit, since the ones digit is equal to the sum of the first two digits.
Consider first those sumleft integers whose hundreds digit is \(1\). We enumerate through the possibilities for the tens digit to determine that the sumleft integers with hundreds digit \(1\) are \(101\), \(112\), \(123\), \(134\), \(145\), \(156\), \(167\), \(178\), and \(189\). Therefore, there are \(9\) sumleft integers with hundreds digit \(1\).
We continue in this manner, and for each possible hundreds digit, we determine all the sumleft integers with that hundreds digit. We have organized this information in the table below.
| Hundreds digit | Sumleft integers | Number of sumleft integers |
|---|---|---|
| \(1\) | \(101\), \(112\), \(123\), \(134\), \(145\), \(156\), \(167\), \(178\), \(189\) | \(9\) |
| \(2\) | \(202\), \(213\), \(224\), \(235\), \(246\), \(257\), \(268\), \(279\) | \(8\) |
| \(3\) | \(303\), \(314\), \(325\), \(336\), \(347\), \(358\), \(369\) | \(7\) |
| \(4\) | \(404\), \(415\), \(426\), \(437\), \(448\), \(459\) | \(6\) |
| \(5\) | \(505\), \(516\), \(527\), \(538\), \(549\) | \(5\) |
| \(6\) | \(606\), \(617\), \(628\), \(639\) | \(4\) |
| \(7\) | \(707\), \(718\), \(729\) | \(3\) |
| \(8\) | \(808\), \(819\) | \(2\) |
| \(9\) | \(909\) | \(1\) |
Therefore, there are \(9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45\) sumleft integers.