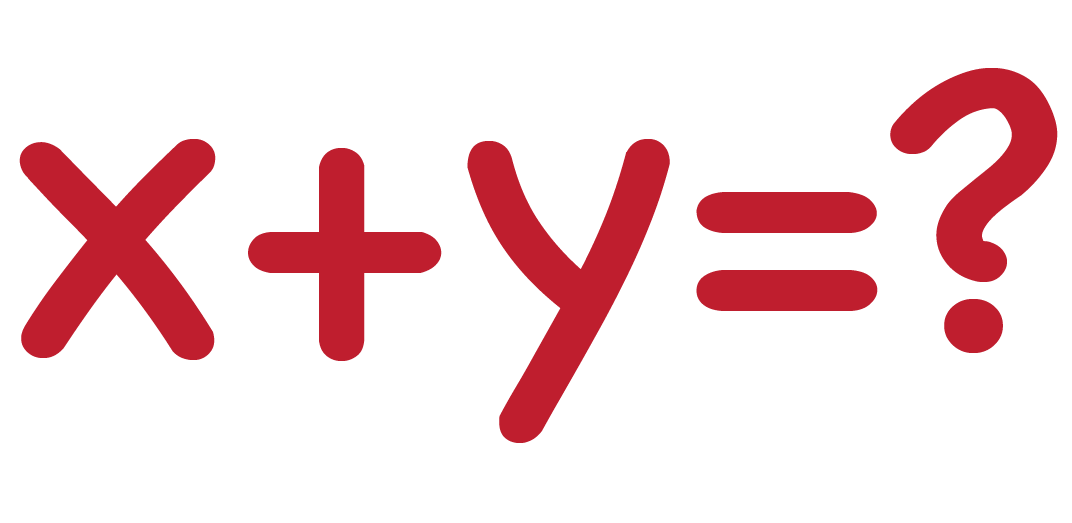

If \(2x=3y+11\) and \(2^x=2^{4(y+1)}\), determine the value of \(x+y\).
Solution 1
Since \(2^x=2^{4(y+1)}\), it follows that \(x=4(y+1)\), or \(x=4y+4\). We now have the following two equations. \[\begin{align*} 2x&=3y+11 \tag{1}\\ x&=4y+4 \tag{2}\end{align*}\] We can substitute equation \((2)\) into equation \((1)\) for \(x\). \[\begin{aligned} 2x&=3y+11\\ 2(4y+4)&=3y+11\\ 8y+8&=3y+11\\ 5y&=3\\ y&=\frac{3}{5}\end{aligned}\] Now, we can substitute \(y=\frac{3}{5}\) into equation \((2)\) to solve for \(x\). \[\begin{aligned} x&=4y+4\\ &=4\left(\frac{3}{5}\right)+4\\ &=\frac{12}{5}+\frac{20}{5}\\ &=\frac{32}{5}\end{aligned}\] Now that we have the values of \(x\) and \(y\), we can determine the value of \(x+y\). \[x+y=\frac{32}{5}+\frac{3}{5}=\frac{35}{5}=7\] Therefore, the value of \(x+y\) is \(7\).
Solution 2
We can solve this problem in a faster way without finding the values of \(x\) and \(y\). Since \(2^x=2^{4(y+1)}\), it follows that \(x=4(y+1)\), or \(x=4y+4\). We now have the following two equations. \[\begin{align*} 2x&=3y+11 \tag{1}\\ x&=4y+4 \tag{2}\end{align*}\] We can subtract equation \((2)\) from equation \((1)\), and obtain the equation \(x=-y+7\). Rearranging this equation gives \(x+y=7\). Therefore, the value of \(x+y\) is \(7\).