Problem of the Week
Problem D and Solution
Everything in its Place 2

Problem

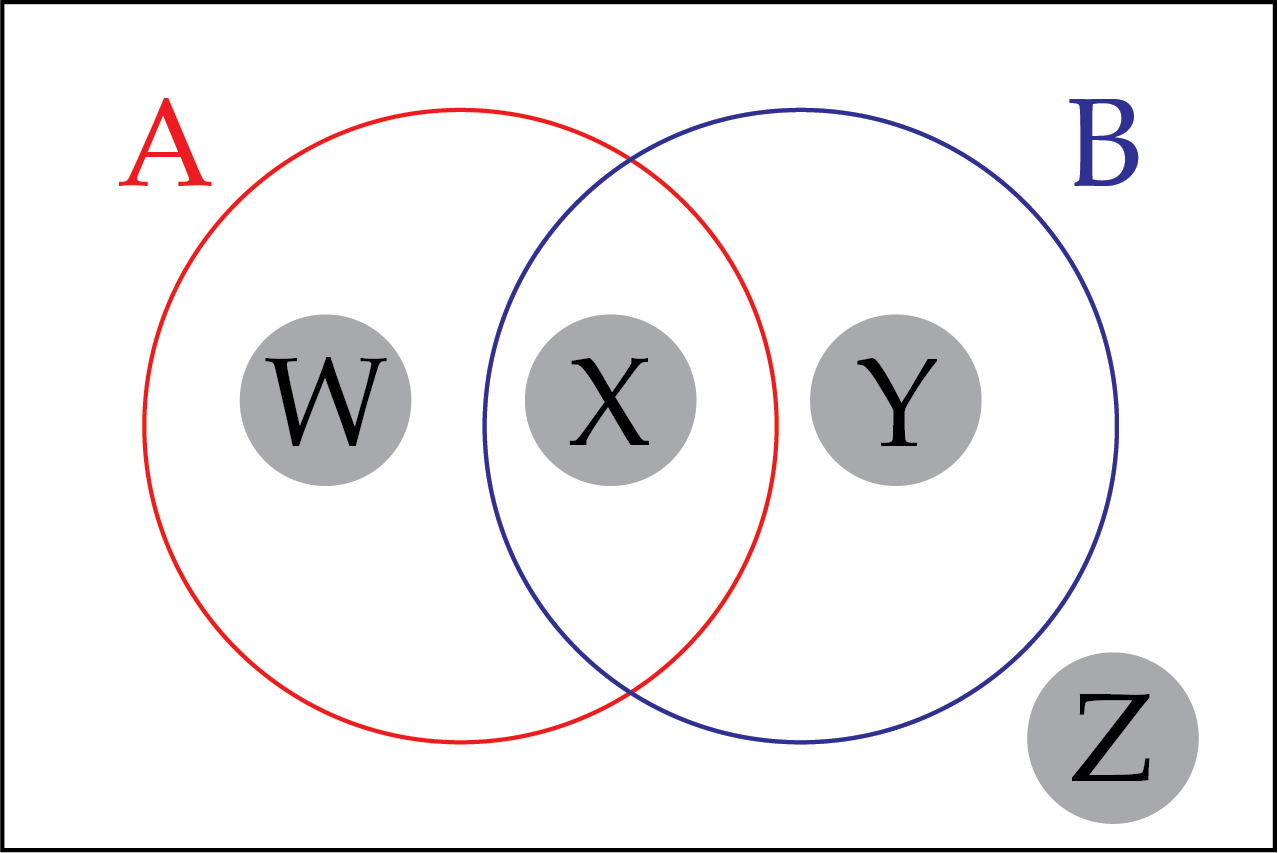
1. A Venn diagram has two circles, labelled A and B.

   

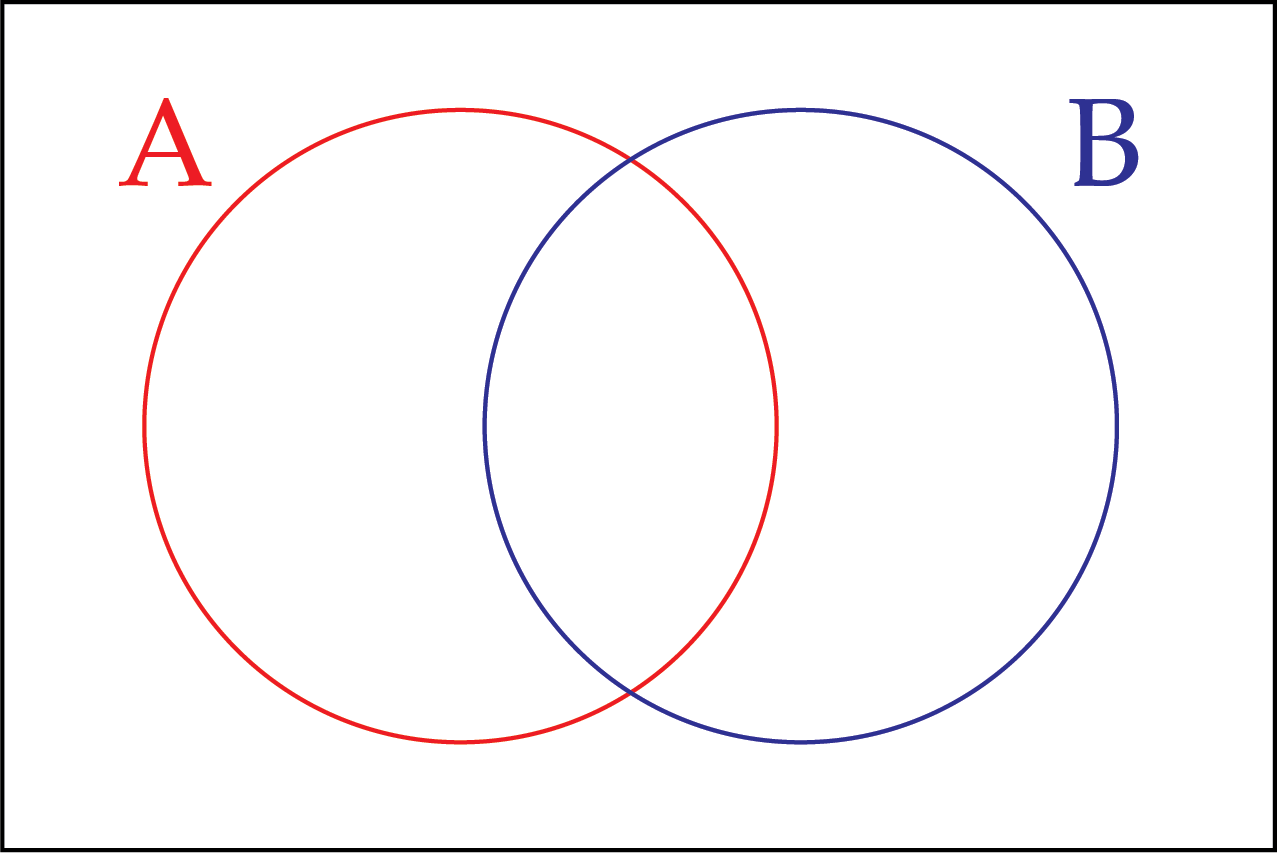
   Each circle contains ordered pairs, \((x,y)\), where \(x\) and \(y\) are real numbers, that satisfy the following criteria.

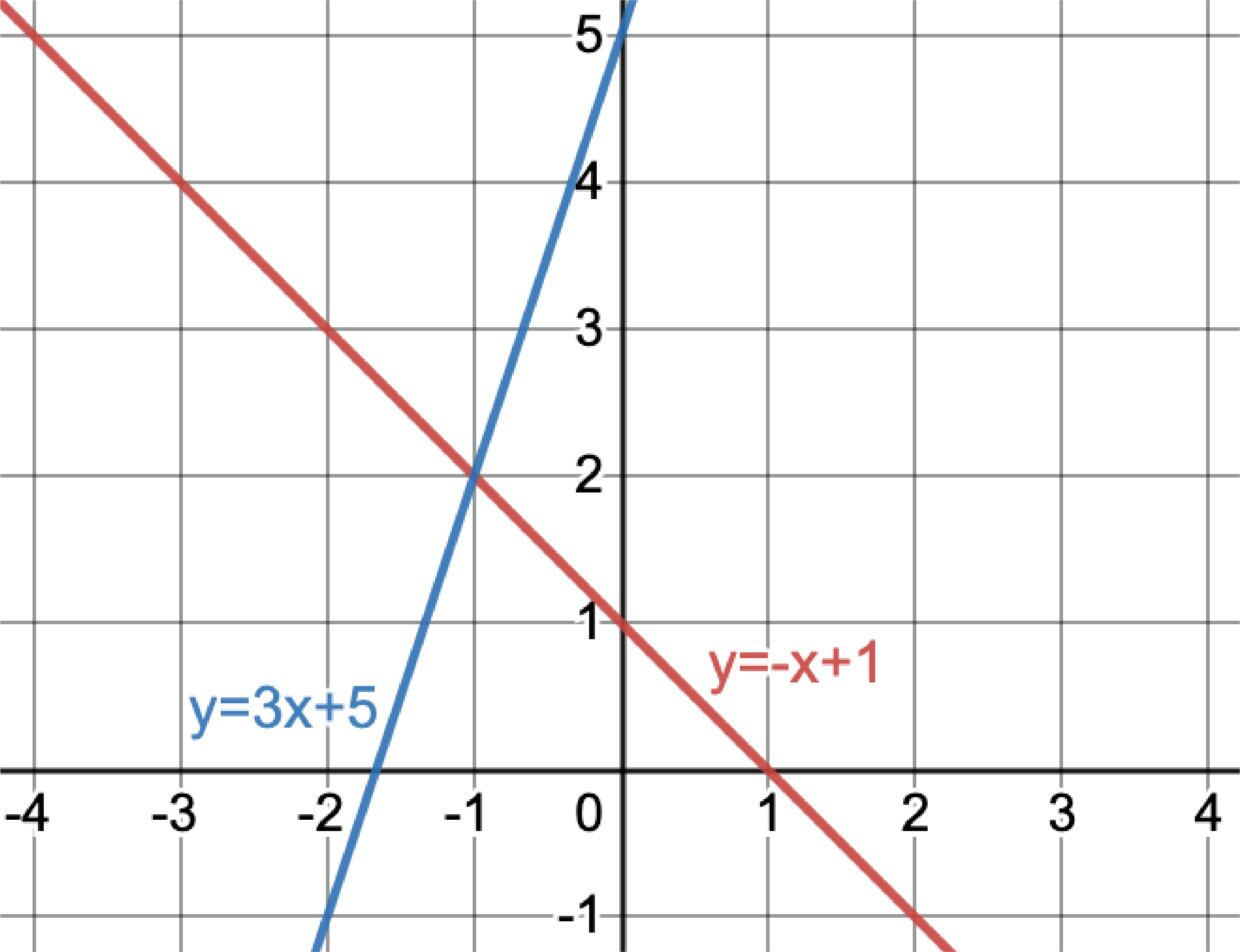
   • A: \(y=-x+1\)

   • B: \(y=3x+5\)

   The overlapping region in the middle contains ordered pairs that are in both A and B, and the region outside both circles contains ordered pairs that are neither in A nor B.

   In total this Venn diagram has four regions. Place ordered pairs in as many of the regions as you can. Is it possible to find an ordered pair for each region?

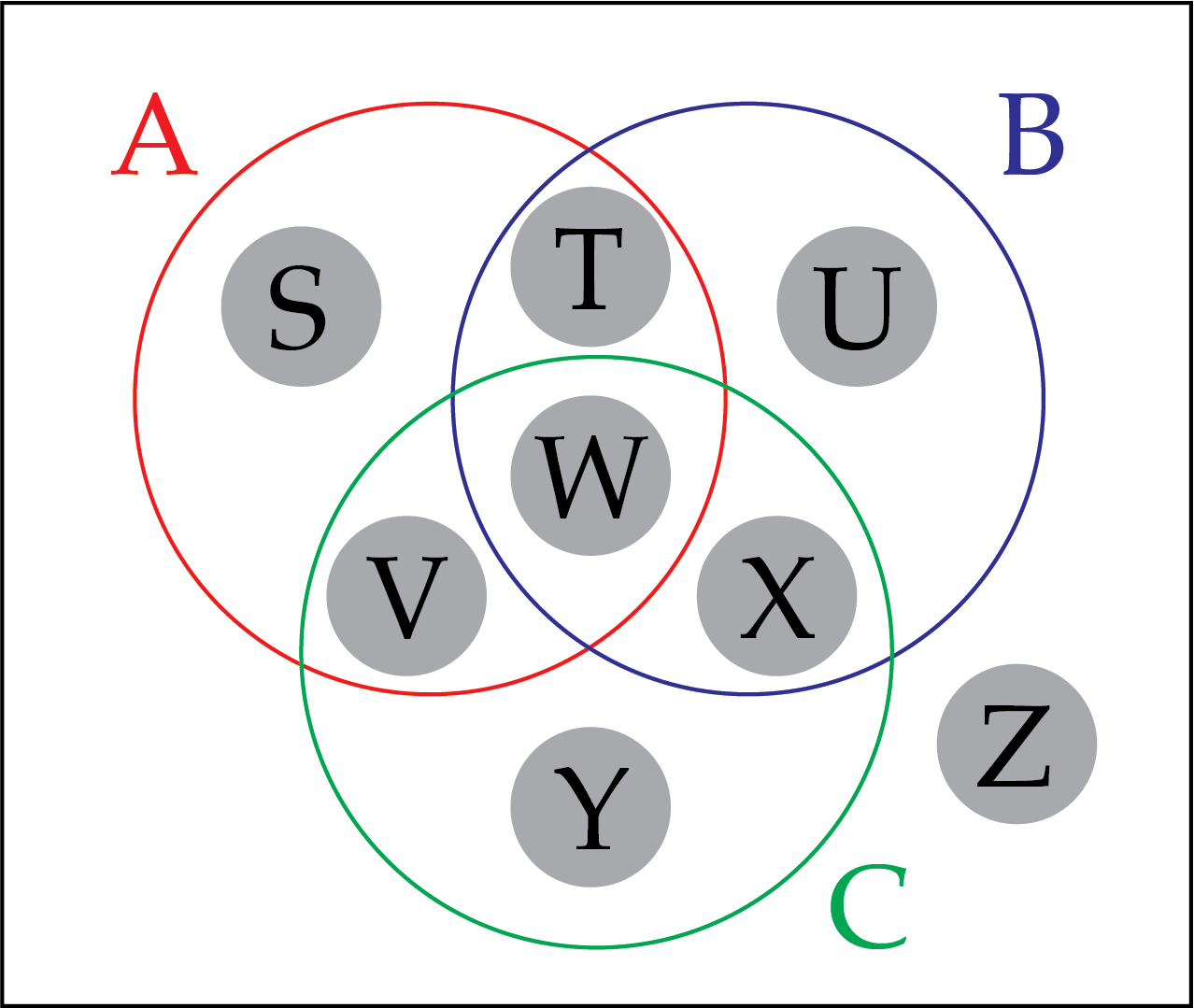
2. A Venn diagram has three circles, labelled A, B, and C.

   

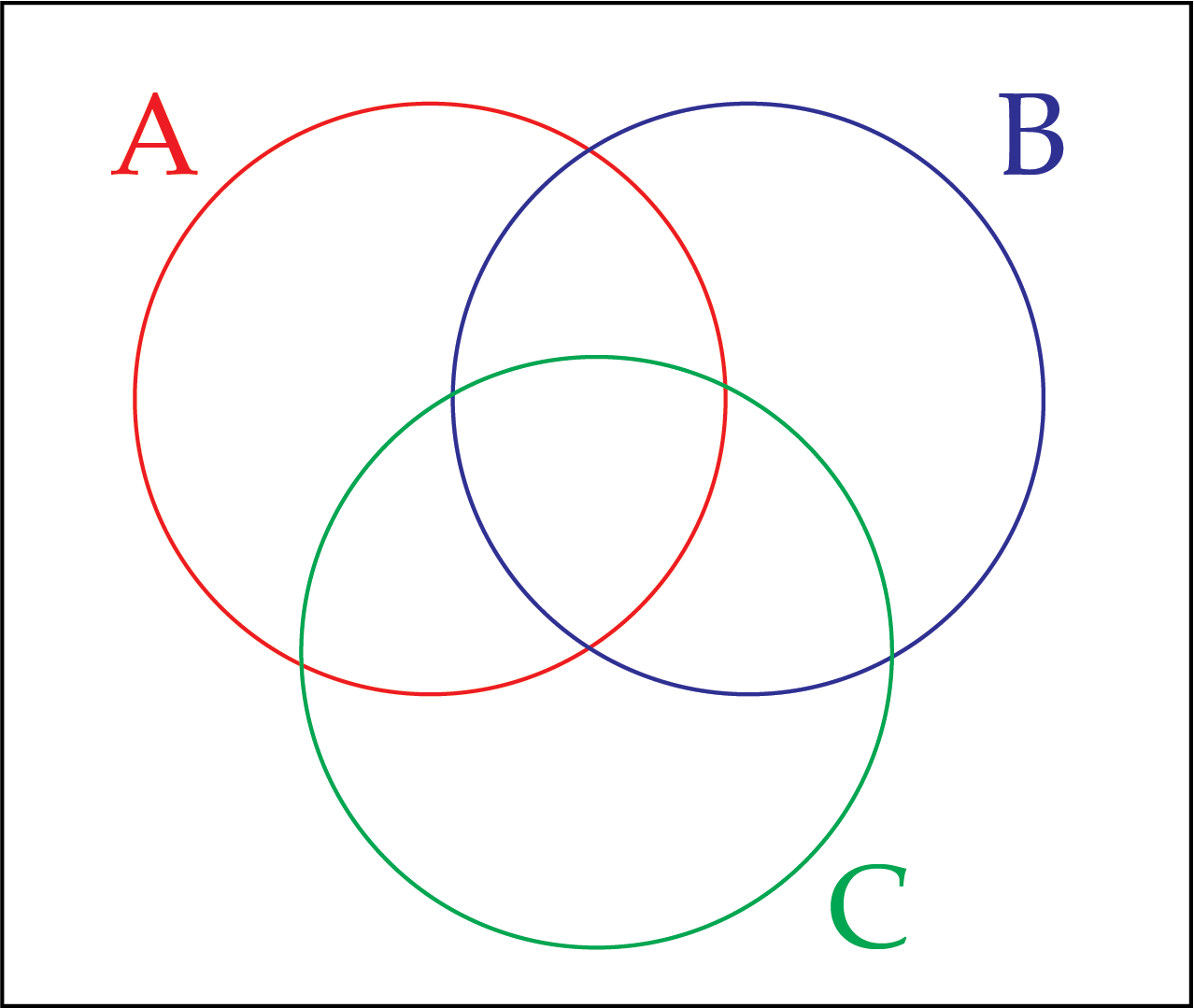
   Each circle contains integers, \(n\), that satisfy the following criteria.

   • A: \(3n<20\)

   • B: \(n+9>6\)

   • C: \(n\) is even

   In total this Venn diagram has eight regions. Place integers in as many of the regions as you can. Is it possible to find an integer for each region?

Solution

1. We have marked the four regions W, X, Y, and Z.

   

   We plot the given equations on a grid as a reference.

   

   • Any ordered pair, \((x,y)\), in region W must satisfy \(y=-x+1\), but not \(y=3x+5\). Any point on the line \(y=-x+1\) that is not on the line \(y=3x+5\) will satisfy this. An example is \((0,1)\).

   • Any ordered pair, \((x,y)\), in region X must satisfy both \(y=-x+1\) and \(y=3x+5\). The only point that satisfies this is the point of intersection, \((-1,2)\).

   • Any ordered pair, \((x,y)\), in region Y must satisfy \(y=3x+5\), but not \(y=-x+1\). Any point on the line \(y=3x+5\) that is not on the line \(y=-x+1\) will satisfy this. An example is \((0,5)\).

   • Any ordered pair, \((x,y)\), in region Z must not satisfy \(y=3x+5\) or \(y=-x+1\). Any point that is not on either line will satisfy this. An example is \((2,2)\).

2. We have marked the eight regions S, T, U, V, W, X, Y, and Z.

   

   Hide/Reveal Description of the Regions

   1. Region S is the region lying inside circle A, outside circle B, and outside circle C.

   2. Region T is inside A, inside B, and outside C.

   3. Region U is inside B, outside A, and outside C.

   4. Region V is inside A, inside C, and outside B.

   5. Region W is inside all three circles.

   6. Region X is inside B, inside C, and outside A.

   7. Region Y inside C, outside A, and outside B.

   8. Region Z is outside all three circles.

   ---

   It is helpful if we first solve the given inequalities.

   \[\begin{aligned} 3n&<20\\ n&<\frac{20}{3}=6\frac{2}{3}\end{aligned}\]

   \[\begin{aligned} n+9&>6\\ n&>-3\end{aligned}\]

   

   • Any integer in region S must be less than \(6\frac{2}{3}\), less than or equal to \(-3\), and an odd number. Any odd integer less than or equal to \(-3\) will satisfy this. An example is \(-5\).

   • Any integer in region T must be less than \(6\frac{2}{3}\), greater than \(-3\), and an odd number. The only integers that satisfy this are \(-1,1,3,\) and \(5\).

   • Any integer in region U must be greater than or equal to \(6\frac{2}{3}\), greater than \(-3\), and an odd number. Any odd integer greater than or equal to \(6\frac{2}{3}\) will satisfy this. An example is \(7\).

   • Any integer in region V must be less than \(6\frac{2}{3}\), less than or equal to \(-3\), and an even number. Any even integer less than or equal to \(-3\) will satisfy this. An example is \(-4\).

   • Any integer in region W must be less than \(6\frac{2}{3}\), greater than \(-3\), and an even number. The only integers that satisfy this are \(-2,0,2,4,\) and \(6\).

   • Any integer in region X must be greater than or equal to \(6\frac{2}{3}\), greater than \(-3\), and an even number. Any even integer greater than or equal to \(6\frac{2}{3}\) will satisfy this. An example is \(8\).

   • Any integer in region Y must be greater than or equal to \(6\frac{2}{3}\), less than or equal to \(-3\), and an even number. No integer satisfies all three conditions, so this region must be left blank.

   • Any integer in region Z must be greater than or equal to \(6\frac{2}{3}\), less than or equal to \(-3\), and an odd number. No integer satisfies all three conditions, so this region must also be left blank.