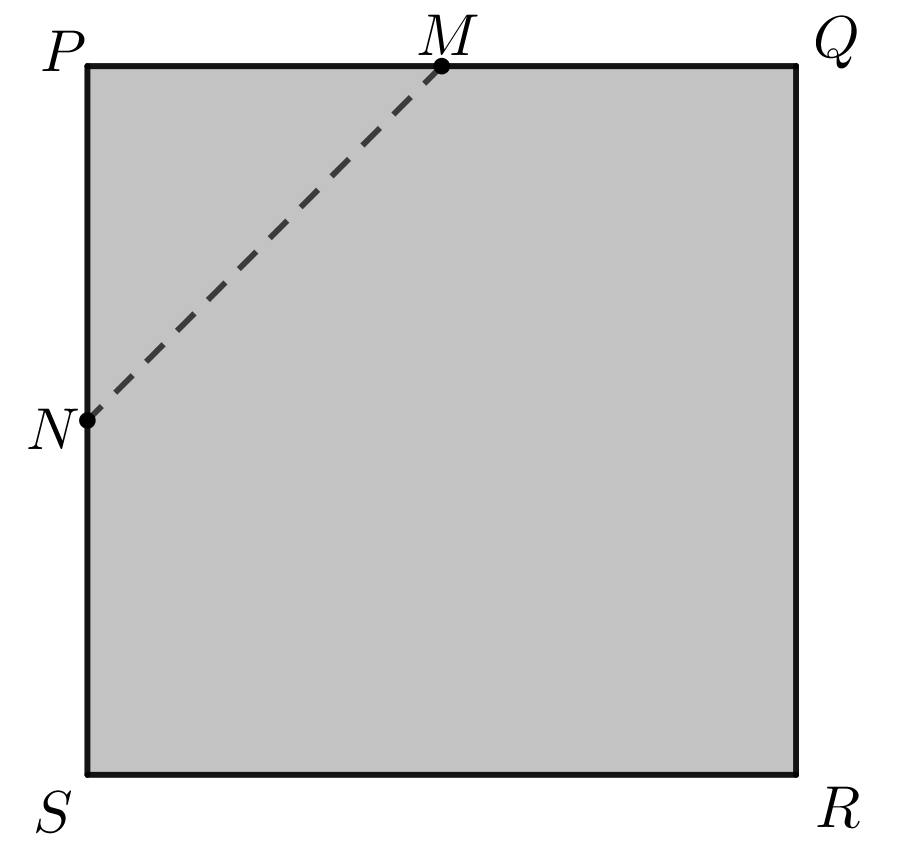

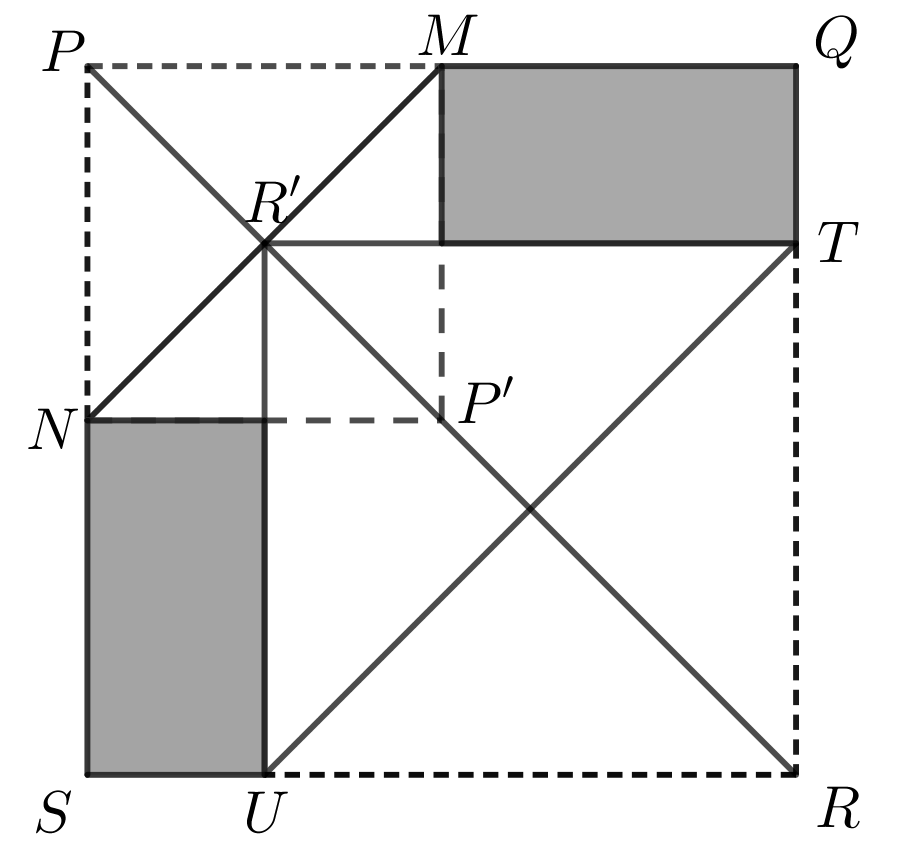
A square piece of paper, \(PQRS\), has side length \(40\) cm. The page is grey on one side and white on the other side. Point \(M\) is the midpoint of side \(PQ\) and point \(N\) is the midpoint of side \(PS\).

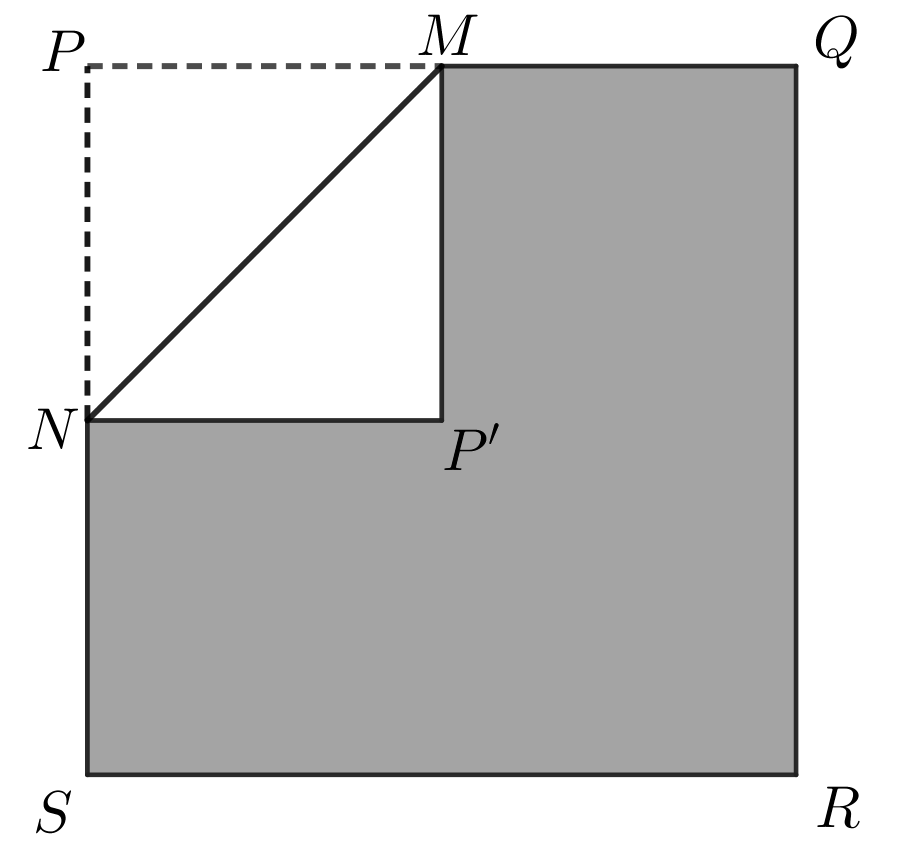
The paper is folded along \(MN\) so that \(P\) touches the paper at the point \(P'\).
Point \(T\) lies on \(QR\) and point \(U\) lies on \(SR\) such that \(TU\) is parallel to \(MN\), and when the paper is folded along \(TU\), the point \(R\) touches the paper at the point \(R'\) on \(MN\).
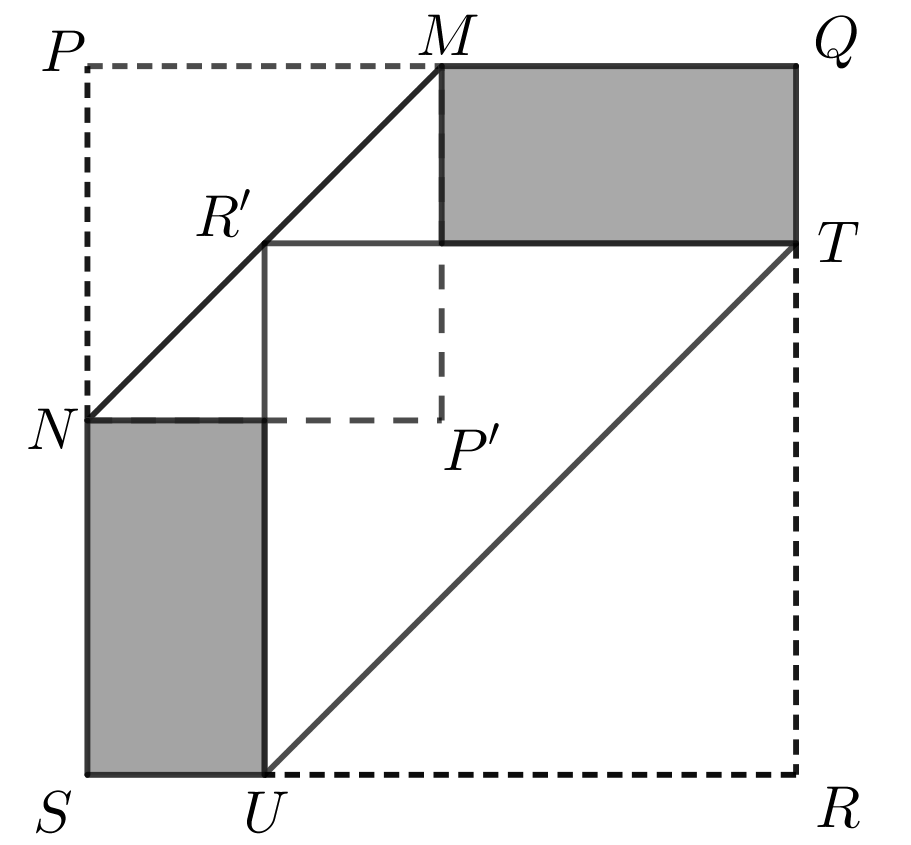
What is the area of hexagon \(NMQTUS\)?
Here are some known properties of the diagonals of a square that may be useful:
the diagonals are equal in length; and
the diagonals right bisect each other; and
the diagonals bisect the corner angles.
To determine the area of hexagon \(NMQTUS\), we will subtract the area of \(\triangle PMN\) and the area of \(\triangle TRU\) from the area of square \(PQRS\).
Since \(M\) and \(N\) are the midpoints of \(PQ\) and \(PS\), respectively, we know \(PM=\frac{1}{2}(PQ)=20\) cm and \(PN=\frac{1}{2}(PS)=20\) cm. Therefore, \(PM=PN=20\) and \(\triangle PMN\) is an isosceles right-angled triangle. It follows that \(\angle PNM=\angle PMN=45\degree\).
After the first fold, \(P\) touches the paper at \(P'\). \(\triangle P'MN\) is a reflection of \(\triangle PMN\) in the line segment \(MN\). It follows that \(\angle P'MN=\angle PMN=45\degree\) and \(\angle P'NM=\angle PNM=45\degree\). Therefore, \(\angle PMP'=\angle PNP'=90\degree\). Since all four sides of \(PMP'N\) are equal in length and all four corners are \(90\degree\), \(PMP'N\) is a square.
Since \(\angle MPP'=\angle MPR=45\degree\), the diagonal \(PP'\) of square \(PMP'N\) lies along the diagonal \(PR\) of square \(PQRS\). Let \(O\) be the intersection of the two diagonals of square \(PMP'N\). It is also the intersection of \(MN\) and \(PR\). (We will show later that this is in fact \(R'\), the point of contact of \(R\) with the paper after the second fold.)
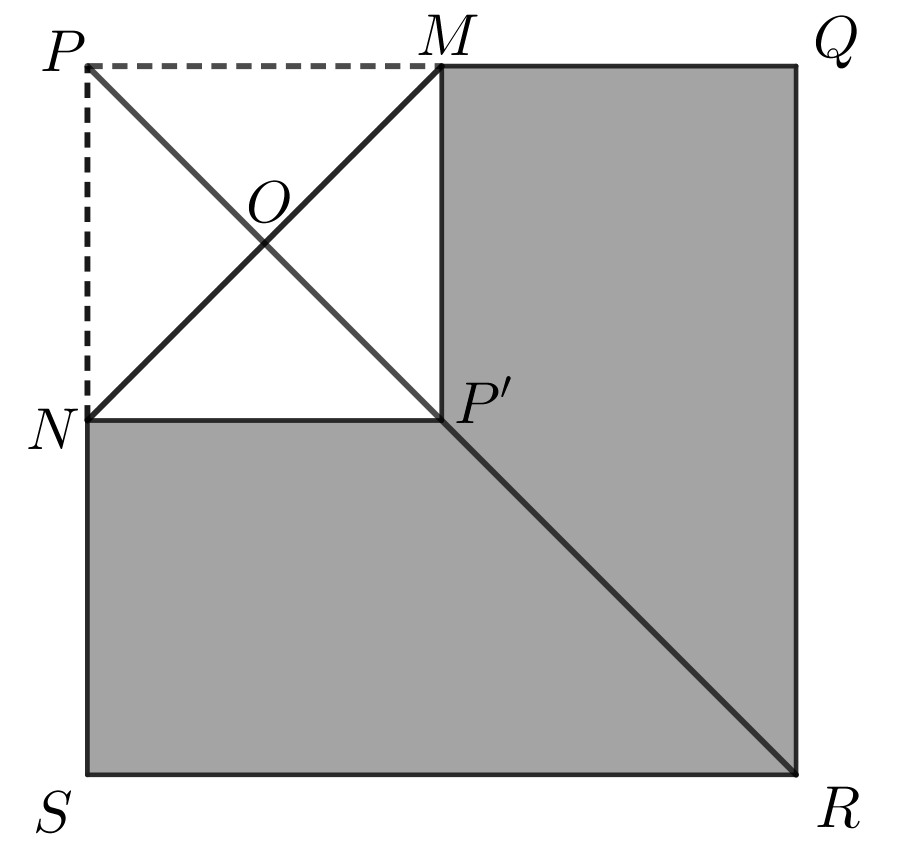
The length of the diagonal of square \(PMP'N\) can be found using the Pythagorean Theorem. \[PP'=\sqrt{(PM)^2+(MP')^2}=\sqrt{20^2+20^2}=\sqrt{800}=\sqrt{400}\sqrt{2}=20\sqrt{2}\]
Thus, \(PO=\frac{1}{2}(PP')=\frac{1}{2}(20\sqrt{2})=10\sqrt{2}\) cm.
In the last two steps of calculating \(PP'\), we simplified the radical. We will do this quite often in the solution. Here is the process to simplify radicals, for students who may not be familiar with this:
Find the largest perfect square that divides into the radicand (the number under the root symbol). In this case, 400 is the largest perfect square that divides 800.
Rewrite the radicand as the product of the perfect square and the remaining factor. In this case, we get \(\sqrt{400\times 2}\).
Take the square root of the perfect square. In this case, we get \(20\sqrt{2}\).
Since \(TU\) is parallel to \(MN\), it follows that \(\angle RTU=\angle RUT=45\degree\) and \(\triangle TRU\) is an isosceles right-angled triangle with \(TR=RU\).
When \(\triangle TRU\) is reflected in the line segment \(TU\) with \(R'\) being the image of \(R\), a square, \(TRUR'\), is created. We will not present the argument here because it is very similar to the argument presented for \(PMP'N\). Since \(\angle TRR'=\angle TRP=45\degree\), \(RR'\) lies along the diagonal \(PR\). Also, \(R'\) lies on \(MN\). This means that \(R'\) and \(O\) are the same point and so \(PR' = PO = 10\sqrt{2}\) cm.
The length of the diagonal of square \(PQRS\) can be calculated using the Pythagorean Theorem. \[PR=\sqrt{(PQ)^2+(QR)^2}=\sqrt{40^2+40^2}=\sqrt{3200}=\sqrt{1600}\sqrt{2}=40\sqrt{2}\]
The length of \(RR'\) equals the length of \(PR\) minus the length of \(PR'\). \[RR'= PR - PR' = 40\sqrt{2}-10\sqrt{2}=30\sqrt{2}\]
But \(RR'=TU\), so \(TU=30\sqrt{2}\) cm. Let \(TR=RU=x\). Then, using the Pythagorean Theorem in \(\triangle TRU\), \[\begin{aligned} (TR)^2+(RU)^2&=(TU)^2\\ x^2+x^2&=(30\sqrt{2})^2\\ x^2+x^2&=900\times 2\\ 2x^2&=1800\\ x^2&=900\end{aligned}\] And since \(x>0\), this gives \(x=30\) cm. We now have enough information to calculate the area of hexagon \(NMQTUS\). \[\begin{aligned} \text{Area }NMQTUS&=\text{Area }PQRS-\text{Area }\triangle PMN-\text{Area }\triangle TRU\\ &=PQ\times QR-\frac{PM\times PN}{2}-\frac{TR\times RU}{2}\\ &=40\times 40-\frac{20\times 20}{2}-\frac{30\times 30 }{2}\\ &=1600-\frac{400}{2}-\frac{900}{2}\\ &=1600-200 - 450\\ &=950\end{aligned}\] Therefore, the area of hexagon \(NMBPQD\) is \(950\text{ cm}^2\).