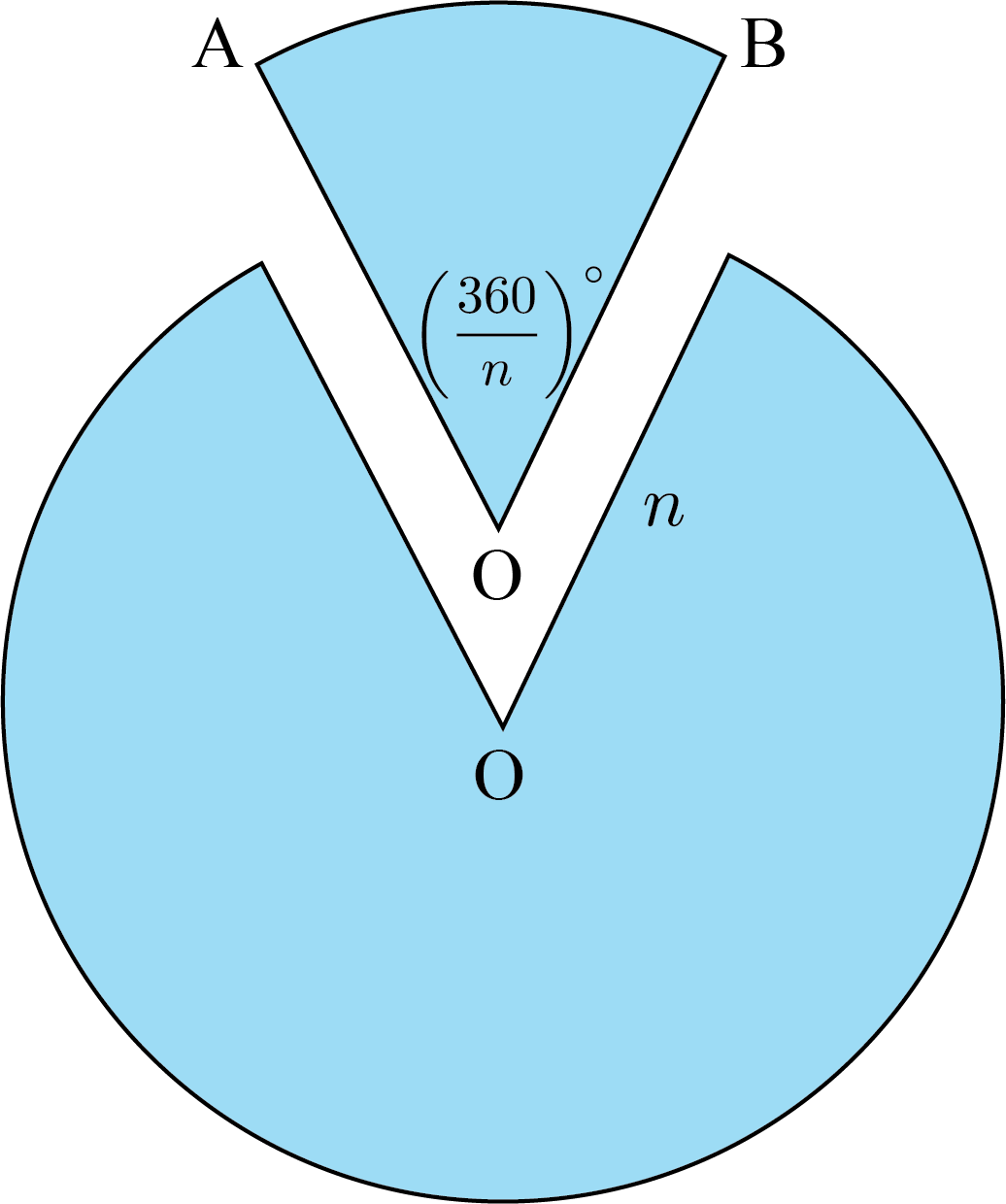

Points \(A\) and \(B\) are on a circle with centre \(O\) and radius \(n\) so that \(\angle AOB=\left(\frac{360}{n}\right) \degree\). Sector \(AOB\) is cut out of the circle.

Determine all positive integers \(n\) for which the perimeter of sector \(AOB\) is greater than \(20\) and less than \(30\).
Note: You may use the fact that the ratio of the length of an arc to the circumference of the circle is the same as the ratio of the sector angle to \(360 \degree\). In fact, the same ratio holds when comparing the area of a sector to the total area of the circle.
In general, as the sector angle gets larger, so does the length of the arc, if the radius remains the same. However in this problem, as the radius \(n\) increases, the sector angle \(\left(\frac{360}{n}\right) \degree\) decreases. So it is difficult to “see” what happens to the length of the arc.
We know the ratio of the arc length to the circumference of the circle is the same as the ratio of the sector angle to \(360 \degree\). That is, \[\frac{\text{arc length of $AB$}}{\text{circumference}}=\frac{\text{sector angle of $AOB$}}{360 \degree}\] Rearranging, we have \[\text{arc length of $AB$}=\frac{\text{sector angle of $AOB$}}{360 \degree}\times \text{circumference}\] We know \(\text{circumference}=\pi d = \pi\times 2n\), since \(d=2n\). Thus, \[\text{arc length of $AB$}=\frac{\frac{360}{n}}{360}\times \pi \times 2n=2\pi\]
Now we can use the arc length to calculate the perimeter of \(AOB\). \[\begin{aligned} \text{perimeter of $AOB$} &=AO+OB+\text{arc length of $AB$}\\ &=n+n+2\pi\\ &=2n+2\pi\end{aligned}\] If the perimeter is greater than \(20\), then \[\begin{aligned} 2n+2\pi&>20\\ n+\pi&>10\\ n&>10-\pi\approx 6.9\end{aligned}\] If the perimeter is less than \(30\), then \[\begin{aligned} 2n+2\pi&<30\\ n+\pi&<15\\ n&<15-\pi\approx 11.9\end{aligned}\]
We want all integer values of \(n\) such that \(n>6.9\) and \(n<11.9\). The only integer values of \(n\) that satisfy these conditions are \(n=7\), \(n=8\), \(n=9\), \(n=10\), and \(n=11\).