

In \(\triangle PQR\), \(\angle PRQ = 90^{\circ}\). An altitude is drawn in \(\triangle PQR\) from \(R\) to \(PQ\), intersecting \(PQ\) at \(S\). A median is drawn in \(\triangle PSR\) from \(P\) to \(SR\), intersecting \(SR\) at \(T\).

If the length of the median \(PT\) is \(39\) and the length of \(PS\) is \(36\), determine the length of \(QS\).
Note: An altitude of a triangle is a line segment drawn from a vertex of the triangle perpendicular to the opposite side. A median is a line segment drawn from a vertex of the triangle to the midpoint of the opposite side.
Since \(T\) is a median in \(\triangle PSR\), \(ST = TR\). Let \(ST=TR = a\). Let \(PR = b\), \(QS = c\), and \(QR = d\). The variables and the given information, \(PS = 36\) and \(PT = 39\), are shown in the diagram.
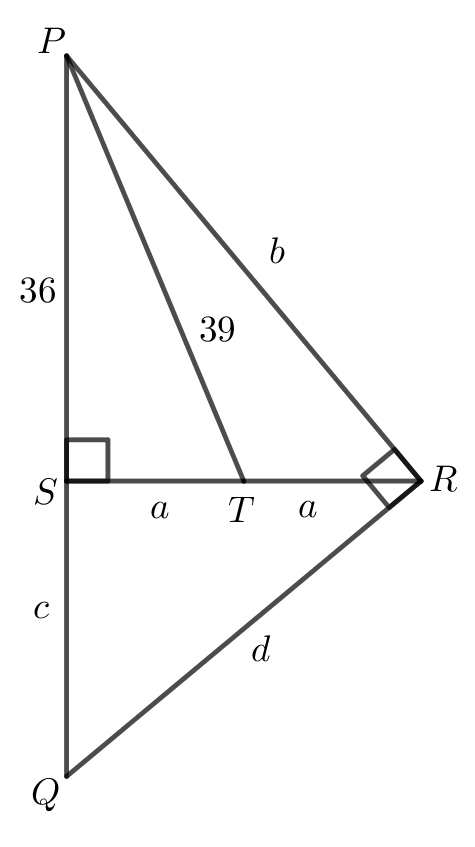
Since \(\triangle PST\) contains a right angle at \(S\), \[\begin{aligned} ST^2 &=PT^2-PS^2\\ a^2&=39^2-36^2\\ &=225\end{aligned}\] Then, since \(a>0\), \(a=15\) follows. Thus, \(SR=2a=30\).
Since \(\triangle PSR\) contains a right angle at \(S\), \[\begin{aligned} PR^2&=PS^2+SR^2\\ b^2&=36^2+30^2\\ &=2196\end{aligned}\] Then, since \(b>0\), \(b=\sqrt{2196}\) follows.
We will now use \(a=15\) and \(b=\sqrt{2196}\) in the three solutions that follow.
Solution 1
In \(\triangle PSR\) and \(\triangle PRQ\), \(\angle PSR=\angle PRQ = 90^{\circ}\) and \(\angle SPR =\angle QPR\), a common angle. So \(\triangle PSR\) is similar to \(\triangle PRQ\).
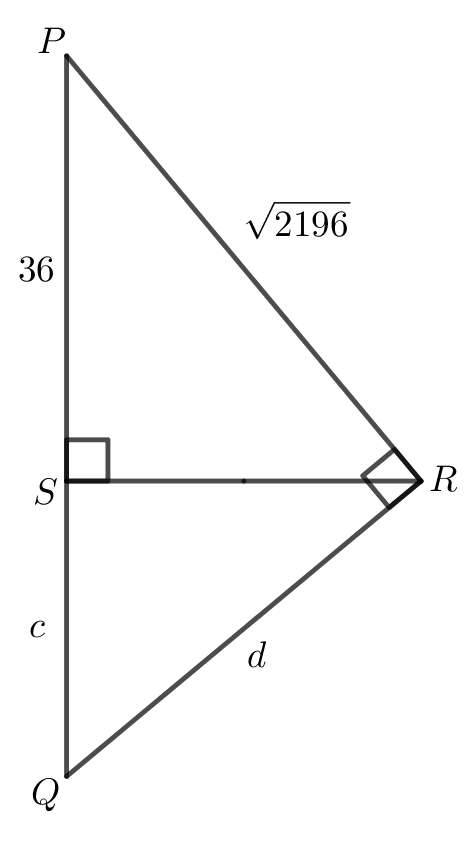
It follows that \[\begin{aligned} \frac{PS}{PR}&=\frac{PR}{PQ}\\ \frac{36}{\sqrt{2196}}&=\frac{\sqrt{2196}}{36+c}\\ 1296+36c&=2196\\ 36c&=900\\ c&=25\end{aligned}\]
Thus, the length of \(QS\) is \(25\).
Solution 2
Since \(\triangle RSQ\) contains a right angle at \(S\), \(QR^2=QS^2+SR^2=c^2+30^2=c^2+900\).
Therefore, \(d^2=c^2+900\).
Since \(\triangle PQR\) contains a right angle at \(R\), \(PQ^2=PR^2+QR^2\). Therefore, \((36+c)^2=(\sqrt{2196})^2+d^2\), which simplifies to \(1296+72c+c^2=2196+d^2\). This further simplifies to \(c^2+72c=900+d^2\).
Substituting \(d^2 = c^2 +900\), we obtain \(c^2+72c=900+c^2+900\). Simplifying, we get \(72c=1800\) and \(c=25\) follows.
Thus, the length of \(QS\) is \(25\).
Solution 3
Position \(\triangle PQR\) on the \(xy\)-plane so that \(PQ\) lies along the \(y\)-axis, and altitude \(SR\) lies along the positive \(x\)-axis with \(S\) at the origin. Then \(P\) has coordinates \((0, 36)\), \(T\) has coordinates \((15,0)\), and \(R\) has coordinates \((30,0)\).
Since \(Q\) is on the \(y\)-axis, let \(Q\) have coordinates \((0,b)\) with \(b<0\).
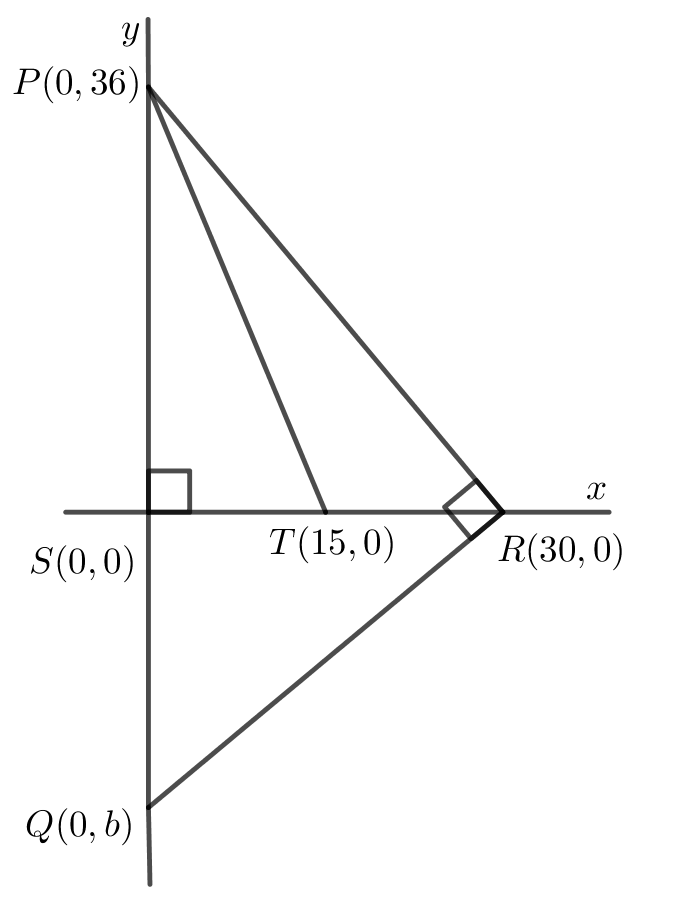
Notice that \[\text{slope }PR=\dfrac{36-0}{0-30}=\dfrac{-6}{5}\text{ and slope }QR=\dfrac{b-0}{0-30}=\dfrac{b}{-30}\]
Since \(\angle PRQ=90^{\circ}\), \(PR\perp QR\), and so their slopes are negative reciprocals of each other. That is, \(\dfrac{b}{-30}=\dfrac{5}{6}\), and so \(b=-25\).
It then follows that the coordinates of \(Q\) are \((0,-25)\). Thus, the length of \(QS\) is \(25\).