Problem of the Week
Problem D
From Square to Hexagon

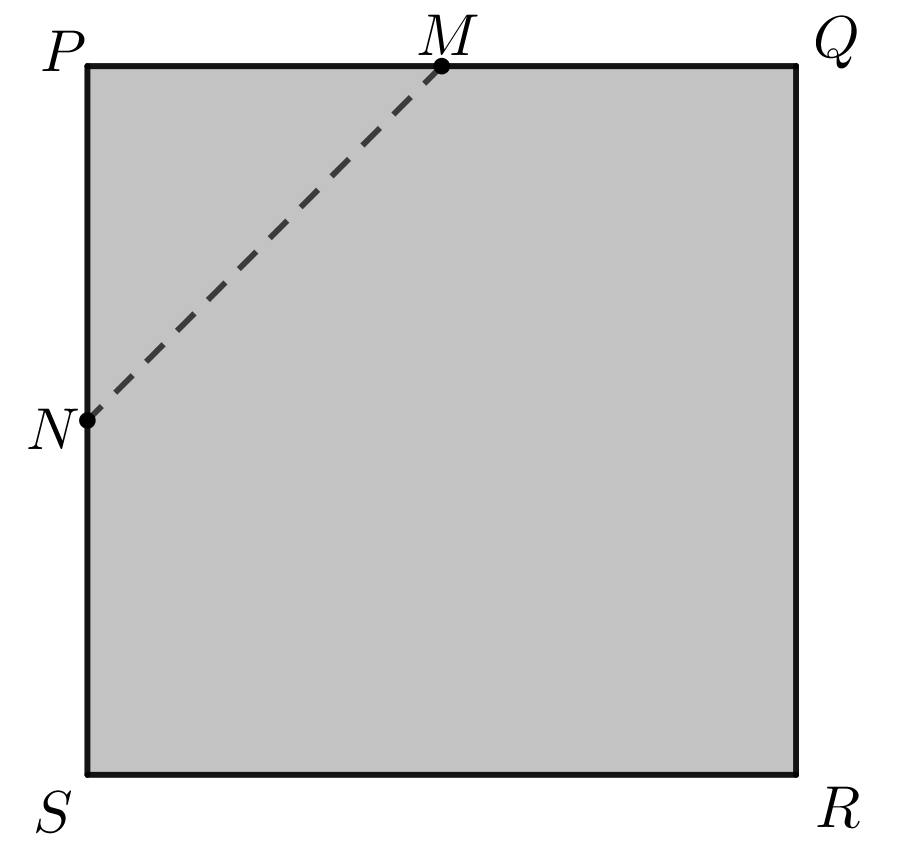
A square piece of paper, \(PQRS\), has side length \(40\) cm. The page is grey on one side and white on the other side. Point \(M\) is the midpoint of side \(PQ\) and point \(N\) is the midpoint of side \(PS\).

The paper is placed grey side up and a dashed line joins points M and N.

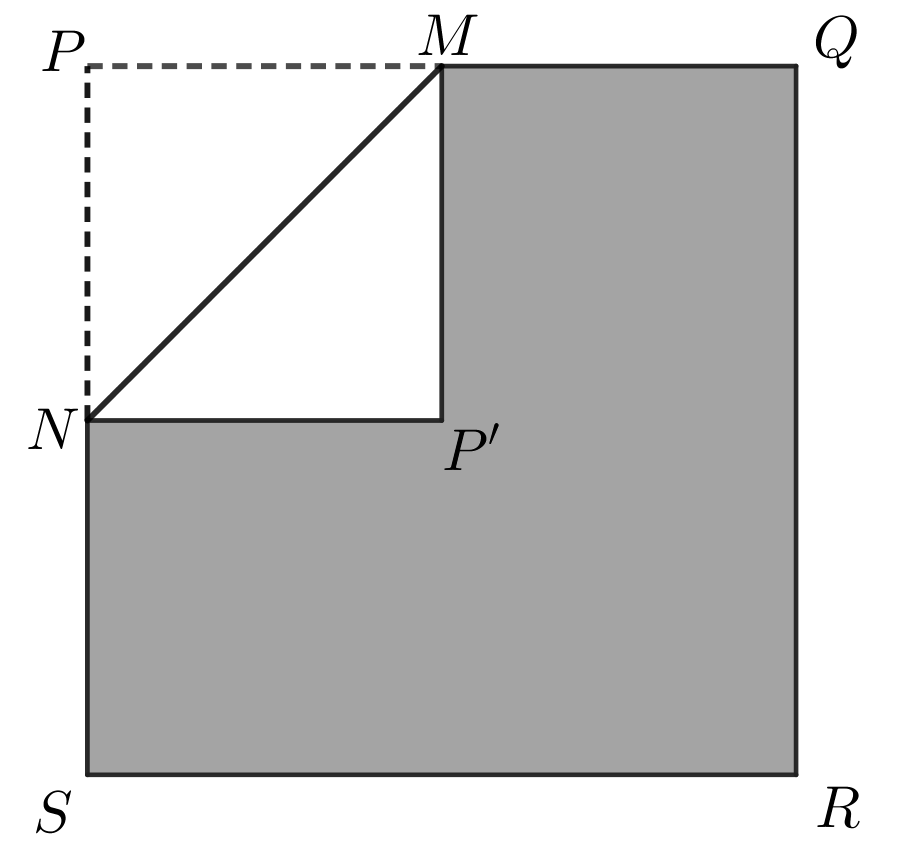
The paper is folded along \(MN\) so that \(P\) touches the paper at the point \(P'\).

The paper after the first fold with dashed line from P to M and P to N. Triangle with vertices N, M, and P prime is white side up.

Point \(T\) lies on \(QR\) and point \(U\) lies on \(SR\) such that \(TU\) is parallel to \(MN\), and when the paper is folded along \(TU\), the point \(R\) touches the paper at the point \(R'\) on \(MN\).

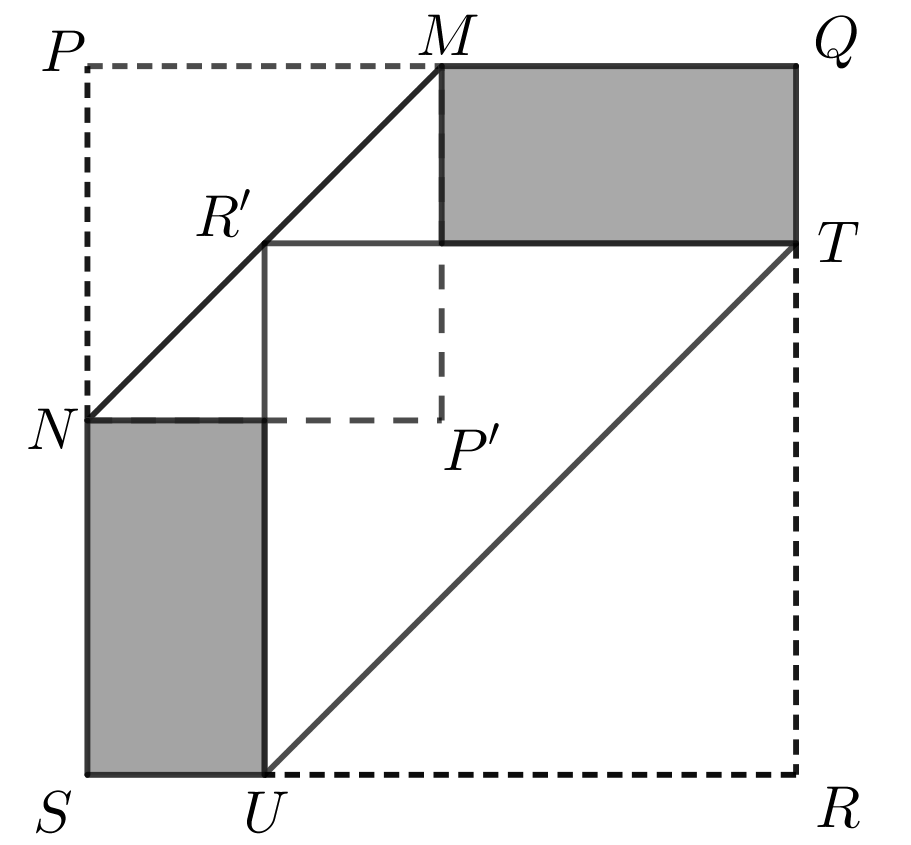
The paper after the second fold with dashed line from R to T and R to U. Triangle with vertices U, T, and R prime is white side up.

What is the area of hexagon \(NMQTUS\)?

Here are some known properties of the diagonals of a square that may be useful:

the diagonals are equal in length; and
the diagonals right bisect each other; and
the diagonals bisect the corner angles.

Problem of the Week Problem D From Square to Hexagon

Problem of the Week
Problem D
From Square to Hexagon