Problem of the Week
Problem D and Solution
Out of This World
Problem
On a far away planet, there are two types of inhabitants: Veres, who always tell the truth, and Nugators, who always lie.
Four of the inhabitants of the planet are seated around a circular table. When asked, “Are you a Vere or a Nugator?”, all four replied, “Vere”. When asked, “Is the person on your right a Vere or a Nugator?”, all four replied, “ Nugator”.
How many Veres are seated at the table? Verify that your solution is the only possible solution.
Solution
There are really five possibilities to check: there could be four Veres, there could be three Veres and one Nugator, there could be two Veres and two Nugators, there could be one Vere and three Nugators, or there could be four Nugators.
We can eliminate cases as follows:
Can two Nugators be seated beside each other?
Suppose there are two Nugators seated beside each other at the table. Since Nugators always lie, when the two Nugators answer the first question, they will both lie and say “Vere”. However, in responding to the second question, the Nugator with the other Nugator on their right would lie and say “Vere”. But everyone responded “Nugator”. This is a contradiction. Therefore, there cannot be two Nugators seated beside each other. This conclusion effectively eliminates the possibility that there are four Nugators, or one Vere and three Nugators.
Can two Veres be seated beside each other?
Suppose there are two Veres seated beside each other at the table. Since Veres always tell the truth, when the two Veres answer the first question, they will both tell the truth and say “Vere”. However, in responding to the second question, the Vere with the other Vere on their right would tell the truth and say “Vere”. But everyone responded “Nugator”. This is a contradiction. Therefore, there cannot be two Veres seated beside each other. This conclusion effectively eliminates the possibility that there are four Veres, or three Veres and one Nugator.
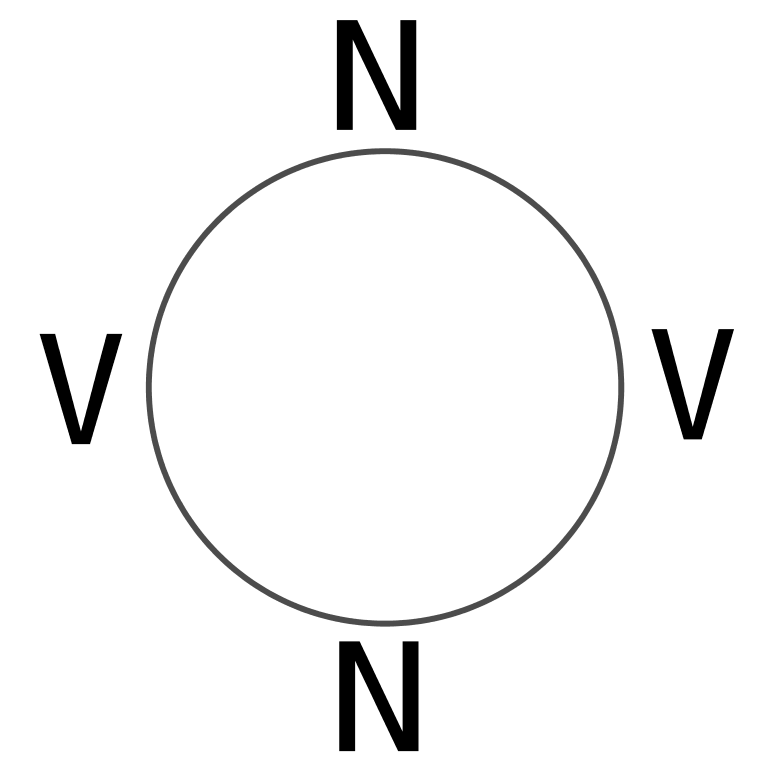
The only possibility left is that there are two Veres and two Nugators seated at the table, and the two Nugators are not sitting next to each other and the two Veres are not sitting next to each other. The diagram illustrates how they must be seated relative to each other.
We can confirm that this arrangement satisfies the problem. Since all Nugators lie and all Veres tell the truth, they will all answer the first question “Vere”. Since all Nugators lie and all Veres tell the truth, they will all answer the second question “Nugator”.
Therefore, there are two Veres and two Nugators, and when seated at a circular table they alternate Vere, Nugator, Vere, Nugator.