

In Canada, pennies are \(1\) cent coins that were used up until \(2012\). Adeline and Bai are playing a game using three pennies and a game board consisting of a row of \(8\) squares. To start the game, the pennies are placed in the three leftmost squares, as shown.

The rules of the game are as follows:
On a player’s turn, the player must move one penny one or more squares to the right.
The penny may not pass over any other penny or land on a square that is occupied by another penny.
The game ends when the pennies are in the three rightmost squares. The last player to move a penny wins the game.
Adeline knows that if she goes first she can always win the game, regardless of where Bai moves the pennies on her turns. Describe Adeline’s first move and her winning strategy.
First, consider playing the game with just two pennies and four squares. We will number the squares from \(1\) to \(4\), starting on the left. The two pennies would start in squares \(1\) and \(2\).
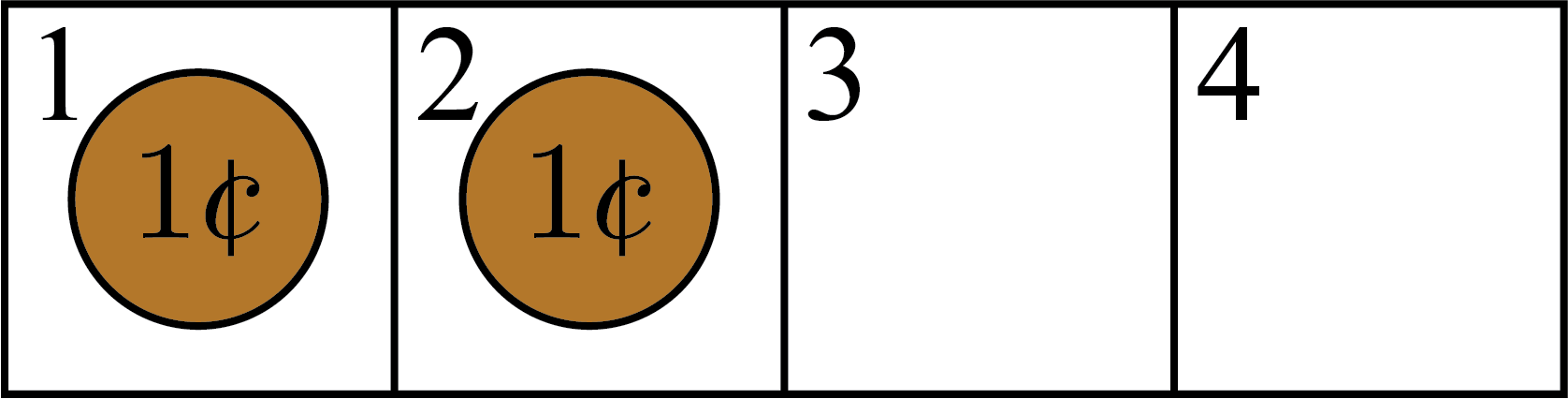
Player \(1\) has two options for their first turn. They can move the penny in square \(2\) to either square \(4\) or square \(3\).
Option 1: Player \(1\) moves the penny in square \(2\) to square \(4\). Then the pennies would be in squares \(1\) and \(4\).
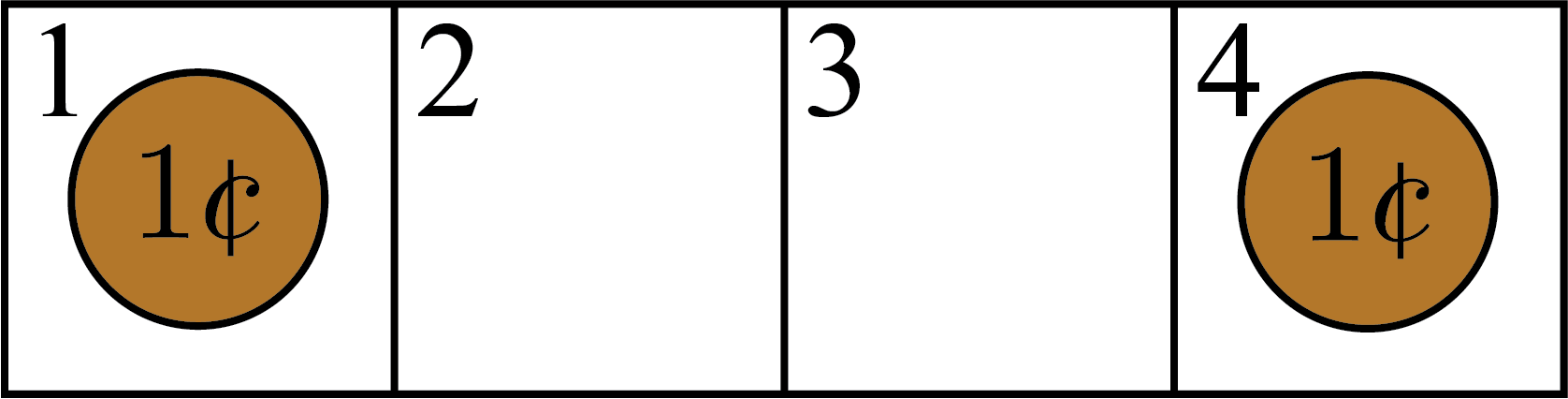
If Player \(2\) moves the penny in square \(1\) to square \(3\), then they would win the game because the pennies would be in squares \(3\) and \(4\).
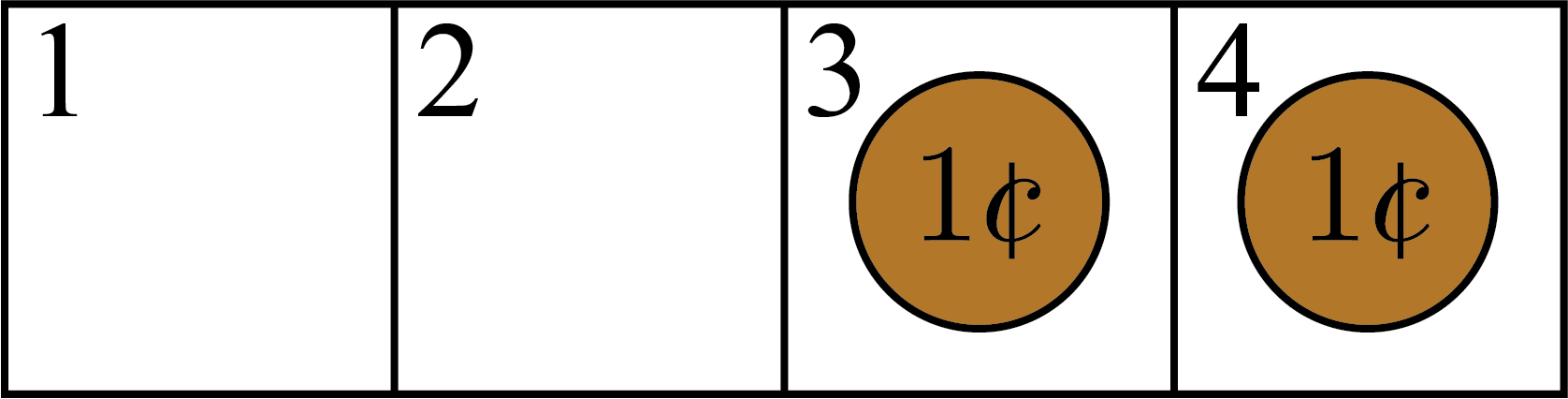
Option 2: Player \(1\) moves the penny in square \(2\) to square \(3\). Then the pennies would be in squares \(1\) and \(3\).
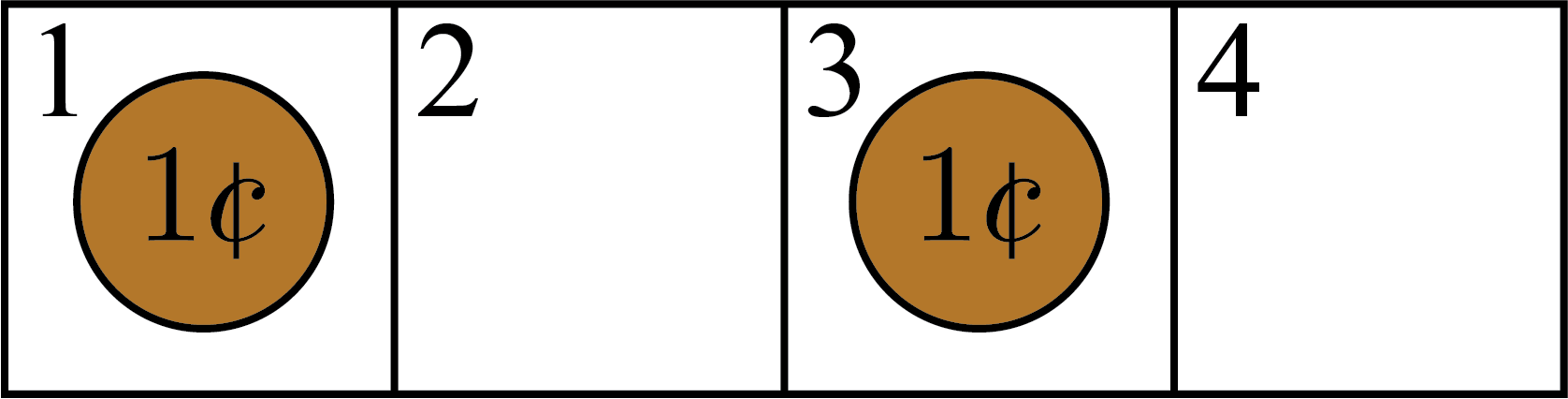
Then Player \(2\) has two options for their turn. They can either move the penny in square \(3\) or move the penny in square \(1\). However, if Player \(2\) wants to win the game, they should not move the penny in square \(3\) to square \(4\). If they do, then the pennies would be in squares \(1\) and \(4\), and then Player \(1\) could move the penny in square \(1\) to square \(3\) and win the game. So, Player \(2\) should move the penny in square \(1\) to square \(2\). Then the pennies would be in squares \(2\) and \(3\).
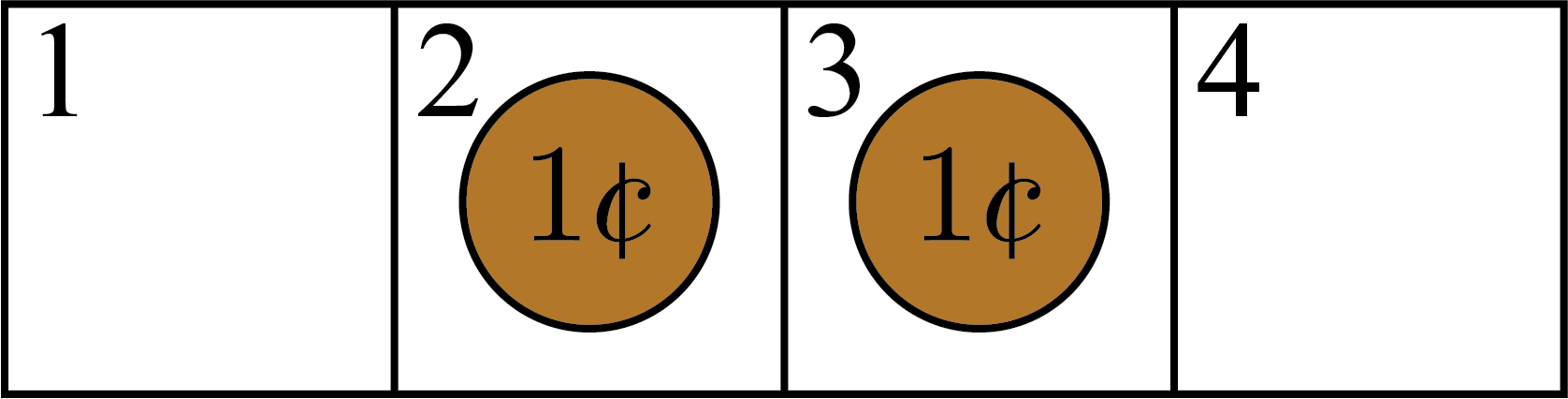
Player \(1\) would be forced to move the penny in square \(3\) to square \(4\). Then the pennies would be in squares \(2\) and \(4\).
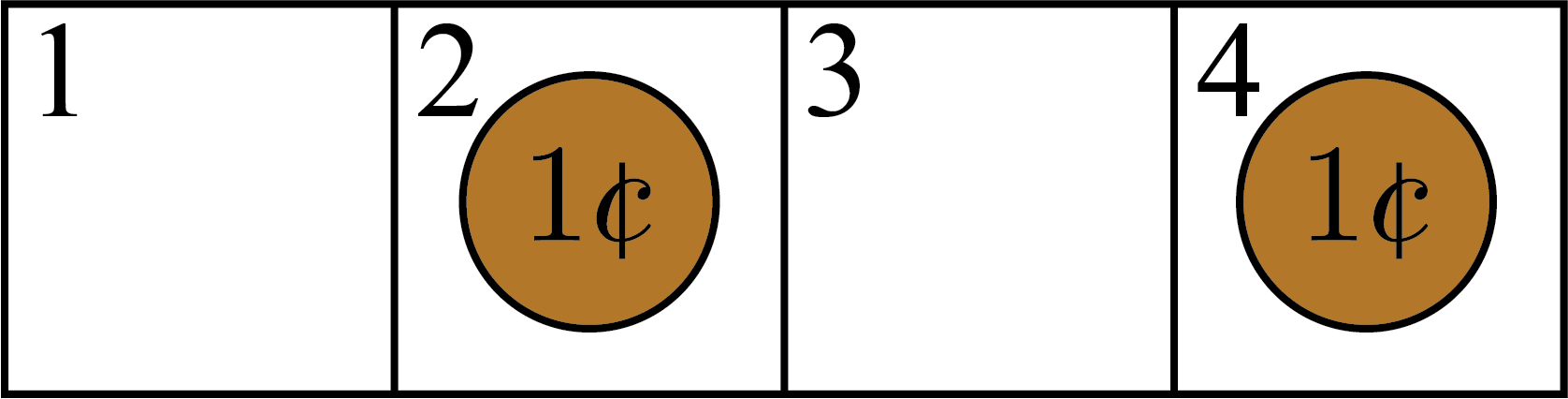
Player \(2\) would then move the penny in square \(2\) to square \(3\), and win the game because the pennies would be in squares \(3\) and \(4\).
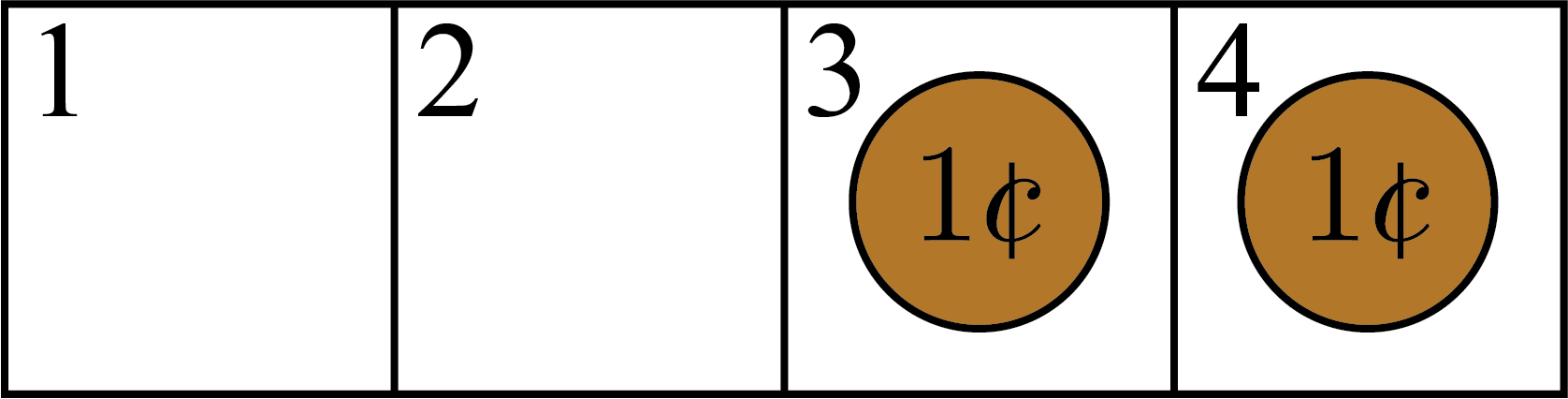
In the game with just two pennies and four squares, Player \(2\) is always able to win, regardless of what Player \(1\) does on their turn. If you look closely, you will see that the winning strategy for Player \(2\) is to copy whatever Player \(1\) did with the other penny. The two pennies start together. Player \(1\) must move the rightmost penny, creating a gap between the two pennies. On the following turn, Player \(2\) can move the other penny in such a way that there is no longer a gap between the two pennies. The number of squares really does not matter. Whatever Player \(1\) does with the penny on the right, Player \(2\) “mimics” with the penny on the left. Player \(2\) wins in this version of the game, but in our game Player \(1\) is supposed to win and we have an extra penny.
In our game, Adeline is Player \(1\) and the pennies start in squares \(1\), \(2\), and \(3\).

If Adeline first moves the penny in square \(3\) to square \(8\), then what is left in squares \(1\) to \(7\) is a two penny game with a total of \(7\) squares.

Now, whatever Bai does on her turn with the penny in square \(2\), Adeline should "mimic" with the penny in square \(1\). This will guarantee that Adeline will win the game.