

Kimi created a digital die that can be controlled with a program. She then programmed it as follows.
Initially it has the numbers \(1\), \(2\), \(3\), \(4\), \(6\), and \(8\) on its faces.
If an odd number is rolled, all the odd numbers on the die double, but the even numbers remain the same.
If an even number is rolled, all the even numbers on the die are halved, but the odd numbers remain the same.
Kimi rolls the die once and the numbers on the die change as described above. She then rolls the die again, but this time something goes wrong and none of the numbers change. What is the probability that she rolled a \(2\) on her second roll?

Solution 1
In this solution, we will determine the possibilities for the first and second roll to count the total number of possible outcomes. We will then count the number of outcomes in which the second roll is a \(2\) and determine the probability.
If the first roll is odd, the numbers on the die change from \(1\), \(2\), \(3\), \(4\), \(6\), \(8\) to \(2\), \(2\), \(6\), \(4\), \(6\), \(8\) as a result of doubling the odd numbers. If we write the possible first and second rolls as an ordered pair, then the following 12 combinations are possible.
\((1,2)\), \((1,2)\), \((1,6)\), \((1,4)\), \((1,6)\), \((1,8)\), \((3,2)\), \((3,2)\), \((3,6)\), \((3,4)\), \((3,6)\), \((3,8)\)
If the first roll is even, the numbers on the die change from \(1\), \(2\), \(3\), \(4\), \(6\), \(8\) to \(1\), \(1\), \(3\), \(2\), \(3\), \(4\) as a result of halving the even numbers. If we write the possible first and second rolls as an ordered pair, then the following 24 combinations are possible.
\((2,1)\), \((2,1)\), \((2,3)\), \((2,2)\), \((2,3)\), \((2,4)\), \((4,1)\), \((4,1)\), \((4,3)\), \((4,2)\), \((4,3)\), \((4,4)\), \((6,1)\), \((6,1)\), \((6,3)\), \((6,2)\), \((6,3)\), \((6,4)\), \((8,1)\), \((8,1)\), \((8,3)\), \((8,2)\), \((8,3)\), \((8,4)\)
There are \(36\) possible outcomes in total. Of these outcomes, \(8\) have a second roll of \(2\). Therefore, the probability of rolling a \(2\) on the second roll is \(\frac{8}{36}=\frac{2}{9}\).
Solution 2
In this solution, we will show the possibilities on a tree diagram.
The probability of rolling an odd number on the first roll is \(\frac{2}{6}=\frac{1}{3}\). The numbers on the die then change from \(1\), \(2\), \(3\), \(4\), \(6\), \(8\) to \(2\), \(2\), \(6\), \(4\), \(6\), \(8\) as a result of doubling the odd numbers. The probability of rolling a \(2\) on the second roll is now \(\frac{2}{6}=\frac{1}{3}\).
The probability of rolling an even number on the first roll is \(\frac{4}{6}=\frac{2}{3}\). The numbers on the die then change from \(1\), \(2\), \(3\), \(4\), \(6\), \(8\) to \(1\), \(1\), \(3\), \(2\), \(3\), \(4\) as a result of halving the even numbers. The probability of rolling a \(2\) on the second roll is now \(\frac{1}{6}\).
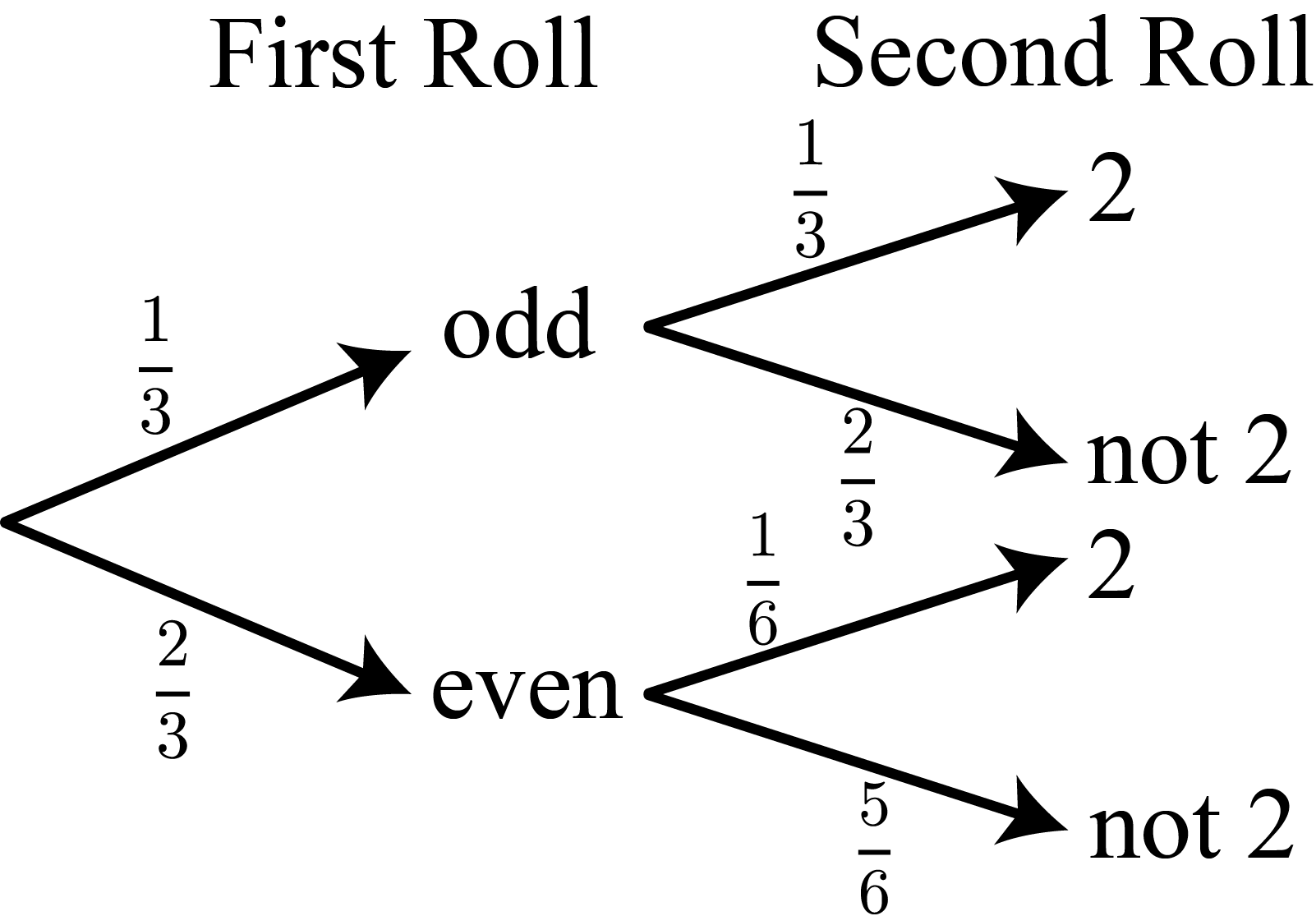
To calculate the probability of rolling an odd number on the first roll and then a \(2\) on the second roll, we multiply the probabilities of each to obtain \(\frac{1}{3}\times \frac{1}{3}=\frac{1}{9}\).
To calculate the probability of rolling an even number on the first roll and then a \(2\) on the second roll, we multiply the probabilities of each to obtain \(\frac{2}{3}\times \frac{1}{6}=\frac{1}{9}\).
Then, to calculate the probability of rolling an odd number on the first roll and then a \(2\) on the second roll, or an even number on the first roll and then a \(2\) on the second roll, we add their probabilities to obtain \(\frac{1}{9}+\frac{1}{9}=\frac{2}{9}\).
Therefore, the probability of rolling a \(2\) on the second roll is \(\frac{2}{9}\).