Solution
Since \(ABCD\) is a rhombus, we know \(AB=BC=CD=DA\). We’re also given that \(AB=AH=HK=KA\). Let \(\angle ADK=x^\circ\).
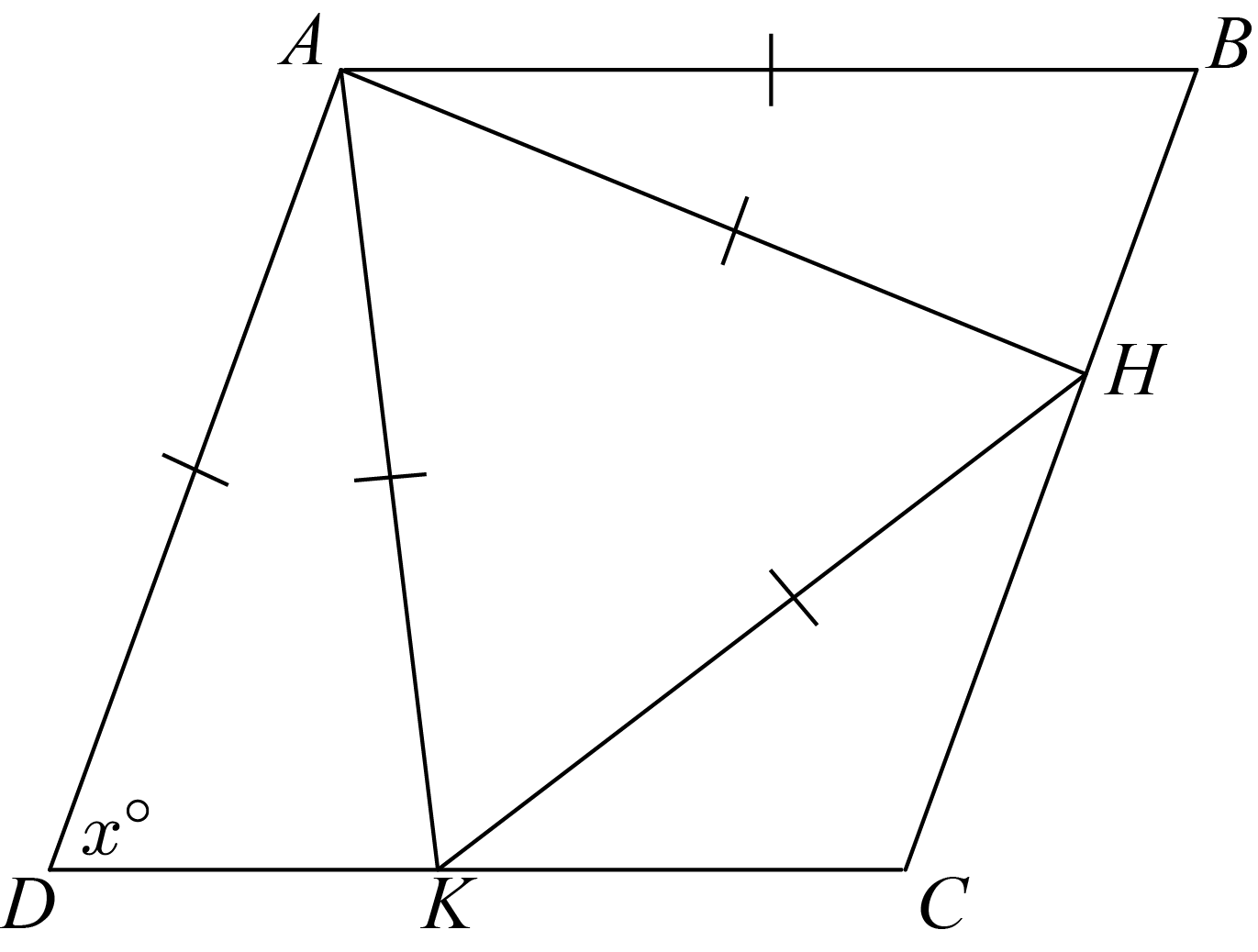
Since \(AH=HK=KA\), \(\triangle AHK\) is an equilateral triangle and each angle in \(\triangle AHK\) is \(60^\circ\). In particular, \(\angle HAK =60^\circ\).
In \(\triangle ADK\), \(AD=AK\) and so \(\triangle ADK\) is isosceles. Therefore, \(\angle AKD=\angle ADK=x^\circ\). Then \(\angle DAK=(180-2x)^\circ\).
Since \(ABCD\) is a rhombus, \(AB \parallel CD\) and \(\angle ADC +\angle BCD=180^\circ\). It follows that \(\angle BCD=(180-x)^\circ\). But in the rhombus we also have \(BC \parallel AD\) and \(\angle BCD +\angle ABC=180^\circ\). It follows that \(\angle ABC=180^\circ-(180-x)^\circ=x^\circ\).
In \(\triangle AHB\), \(AH=AB\) and so \(\triangle AHB\) is isosceles. Therefore, \(\angle AHB=\angle ABH=x^\circ\). Then \(\angle BAH=(180-2x)^\circ\).
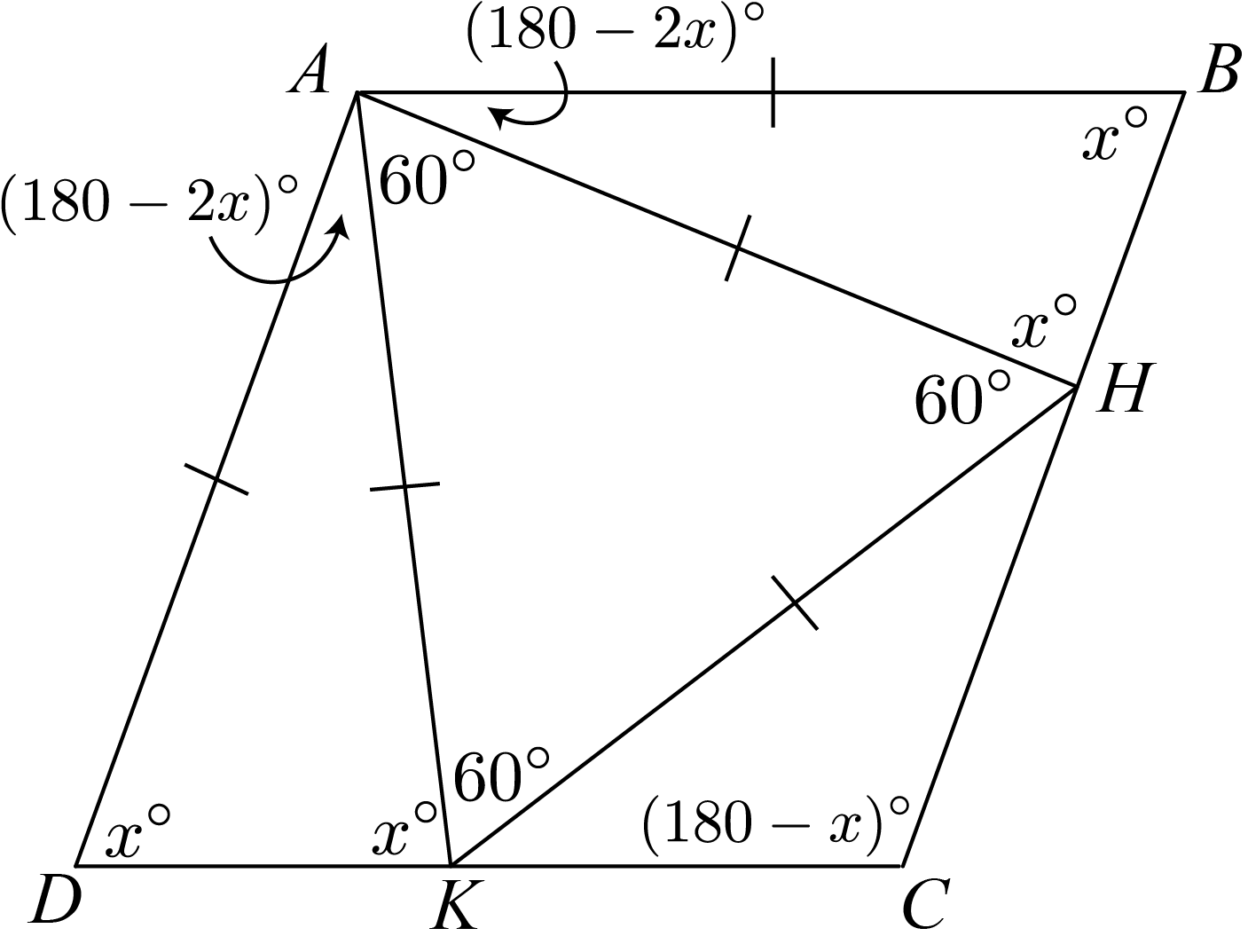
Since \(ABCD\) is a rhombus, \(BC\parallel AD\), so \[\begin{aligned} \angle BAD &=180^\circ-\angle ABC\\ (180-2x)^\circ+60^\circ+(180-2x)^\circ&=180^\circ-x^\circ\\ (420-4x)^\circ&=(180-x)^\circ\\ 240^\circ&=(3x)^\circ\\ x^\circ&=80^\circ\end{aligned}\]
It follows that \[\begin{aligned} \angle BAD &=(180-x)^\circ\\ &=180^\circ-80^\circ\\ &=100^\circ\end{aligned}\]
Therefore, \(\angle BAD=100^\circ\).
