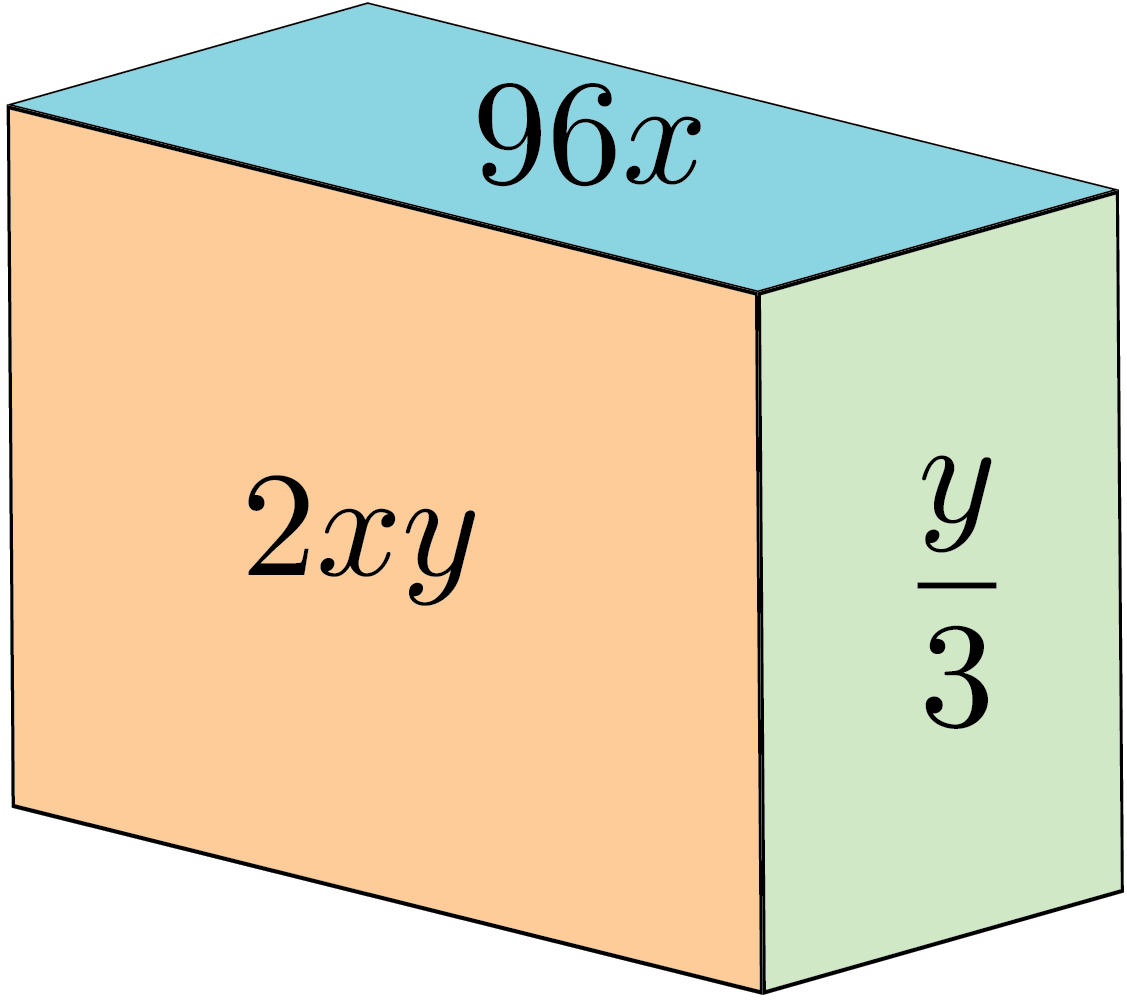

The areas of the front, side, and top faces of a rectangular prism are \(2xy\), \(\dfrac{y}{3}\), and \(96x\text{ cm}^2\), respectively.

Calculate the volume of the rectangular prism in terms of \(x\) and \(y\).
Since \(\frac{y}{3}\) and \(96x\) are areas, then \(x\) and \(y\) must be positive. Let the length, width, and height of the rectangular prism be \(a\), \(b\), and \(c\), respectively.
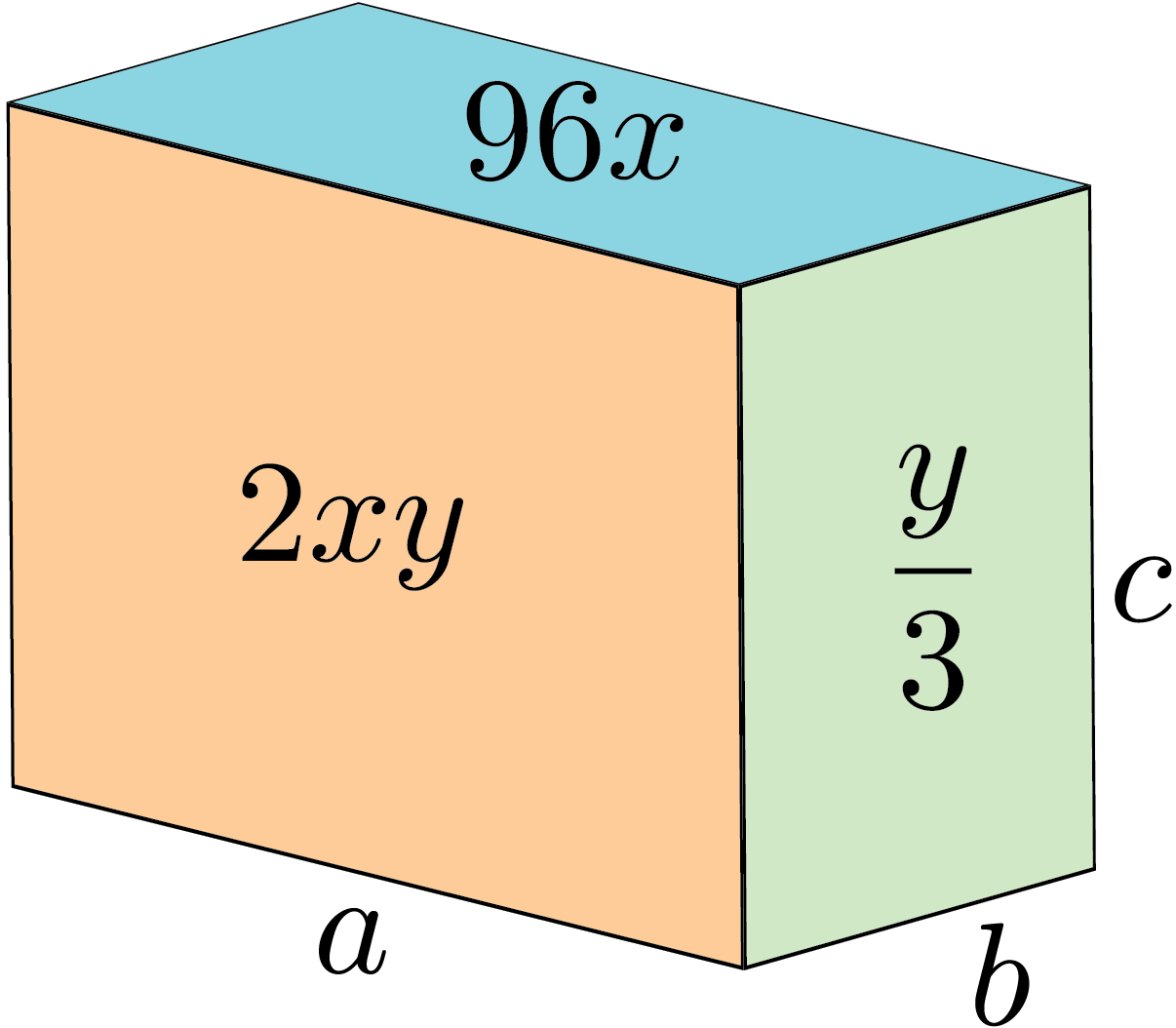
The volume is equal to the product \(abc\).
By multiplying side lengths, we can write the following three equations using the given areas. \[\begin{aligned} ac &= 2xy\\ bc &= \frac{y}{3}\\ ab &= 96x\end{aligned}\] Multiplying the left sides and multiplying the right sides of each of the three equations gives us the following. \[\begin{aligned} (ac)(bc)(ab) &= (2xy)\left(\frac{y}{3}\right)(96x)\\ a^2b^2c^2 &= 64x^2y^2\\ (abc)^2 &= (8xy)^2\\ \sqrt{(abc)^2} &= \pm~\sqrt{(8xy)^2}\\ abc &= \pm ~8xy\end{aligned}\] Since all quantities are positive, we can conclude that \(abc=8xy\).
Therefore, the volume of the rectangular prism is \(8xy~\text{cm}^3\).