

Geocaching is a kind of outdoor treasure hunt where people use GPS devices to look for hidden objects, called caches. In Cartesian Geocaching, instead of using a GPS device, locations are described using Cartesian coordinates.
Hilde sets up a large field for Cartesian Geocaching, measuring the distances in kilometres so that the point \((1,0)\) lies \(1\) km east of the point \((0,0)\), for example.
Hilde starts at point \(A(0,0)\), then walks northwest in a straight line to some point \(B\), where she hides a cache. Then, from \(B\), she walks northeast in a straight line to point \(C(0,4)\) where she hides another cache. Finally she walks straight back to point \(A\).
How far does Hilde walk in total?

We will show four different solutions to this problem.
Solution 1
If you travel northwest from \(A (0,0)\), the line of travel will make a \(45^\circ\) angle with the positive \(y\)-axis. Point \(B\) is located somewhere on this line of travel. If you travel northeast from point \(B\) to \(C(0,4)\), the line will intersect the \(y\)-axis at a \(45^\circ\) angle.
In \(\triangle ABC\), \(\angle BAC=\angle BCA=45^\circ\). It follows that \(\triangle ABC\) is isosceles. Since two of the angles in \(\triangle ABC\) are \(45^\circ\), then the third angle, \(\angle ABC=90^\circ\) and the triangle is right-angled.
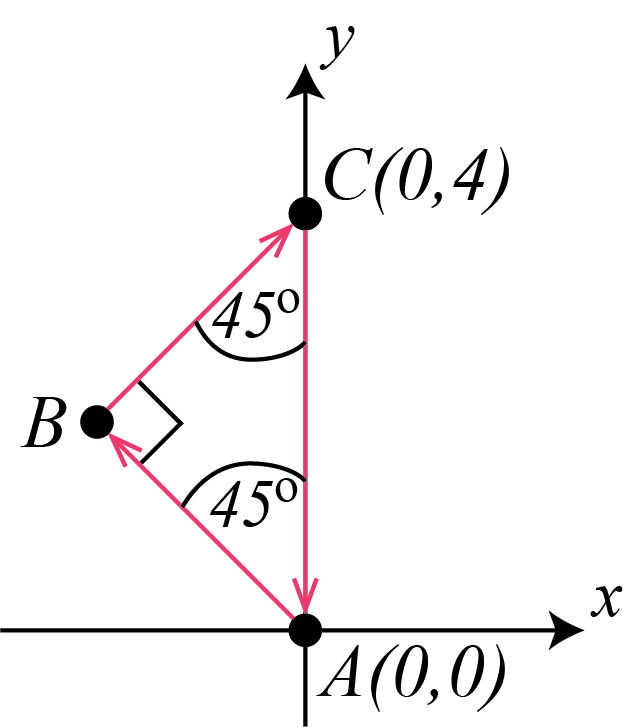
The distance from point \(A\) to point \(C\) along the \(y\)-axis is \(AC=4\) km. Let \(BC=AB=m\), for some \(m>0\). Using the Pythagorean Theorem, we can find the value of \(m\). \[\begin{aligned} AC^2&=BC^2+AB^2\\ 4^2&=m^2+m^2\\ 16&=2m^2\\ 8&=m^2\end{aligned}\]
Then since \(m>0\), we have \(m=\sqrt{8}\).
Thus, the total distance walked by Hilde is \(AB+BC+AC=\sqrt{8}+\sqrt{8}+4=(2\sqrt{8}+4)\) km.
Note that the answer \(\left(2\sqrt{8}+4\right)\) is an exact answer. We can use a calculator to determine that this distance is approximately \(9.7\) km.
The exact total distance travelled can be further simplified as follows: \[2\sqrt{8}+4=2(\sqrt{4}\sqrt{2})+4=2(2\sqrt{2})+4=4\sqrt{2}+4\] This method of simplifying radicals is developed in later mathematics courses.
Solution 2
If you travel northwest from \(A (0,0)\), the line of travel will make a \(45^\circ\) angle with the positive \(y\)-axis. Point \(B\) is located somewhere on this line of travel.
From \(B\), draw a line segment perpendicular to the \(y\)-axis, meeting the \(y\)-axis at point \(D\). A line of travel in a northeast direction from point \(B\) to \(C\) will make \(\angle DBC=45^\circ\).
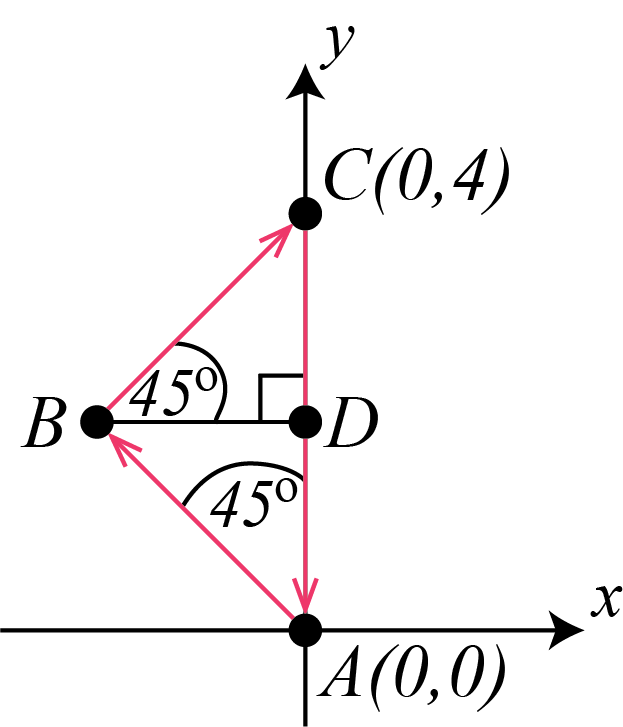
In \(\triangle ABD\), \(\angle BAD=45^\circ\) and \(\angle ADB=90^\circ\). It follows that \(\angle ABD=45^\circ\), \(\triangle ABD\) is isosceles and \(BD=AD\).
In \(\triangle CBD\), \(\angle CBD=45^\circ\) and \(\angle CDB=90^\circ\). It follows that \(\angle BCD=45^\circ\), \(\triangle CBD\) is isosceles and \(CD=BD\).
The distance from point \(A\) to point \(C\) along the \(y\)-axis is \(AC=4\) km. Since \(CD=AD\) and \(AC=CD+AD\), then we know that \(CD=AD=2\) km. But \(CD=BD\) so \(CD=BD=AD=2\) km.
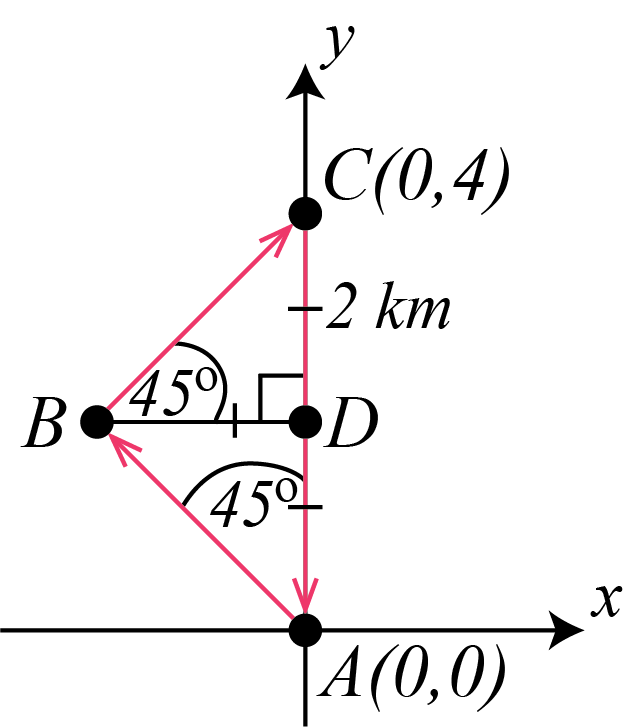
Using the Pythagorean Theorem in right-angled \(\triangle ABD\), we can calculate the length of \(AB\). \[\begin{aligned} AB^2&=BD^2+AD^2\\ AB^2&=2^2+2^2\\ AB^2&=8\end{aligned}\]
Then since \(AB>0\), we have \(AB=\sqrt{8}\).
Using the same reasoning in \(\triangle CBD\), we obtain \(BC=\sqrt{8}\).
Thus, the total distance walked by Hilde is \(AB+BC+AC=\sqrt{8}+\sqrt{8}+4=(2\sqrt{8}+4)\) km.
Note that the answer \(\left(2\sqrt{8}+4\right)\) is an exact answer. We can use a calculator to determine that this distance is approximately \(9.7\) km.
The exact total distance travelled can be further simplified as follows: \[2\sqrt{8}+4=2(\sqrt{4}\sqrt{2})+4=2(2\sqrt{2})+4=4\sqrt{2}+4\] This method of simplifying radicals is developed in later mathematics courses.
Solution 3
If you travel northwest from \(A (0,0)\), the line of travel will make a \(45^\circ\) angle with the positive \(y\)-axis. It follows that this line has slope \(-1\). Since this line passes through \(A(0,0)\) and has slope \(-1\), the equation of the line through \(A\) and \(B\) is \(y=-x\).
Point \(B\) is located somewhere on \(y=-x\). A line drawn to the northeast would be perpendicular to a line drawn to the northwest. Since a line to the northwest has slope \(-1\), it follows that a line to the northeast would have slope \(1\). This second line passes through \(B\) and \(C\), so it has slope \(1\) and \(y\)-intercept \(4\), the \(y\)-coordinate of \(C\). The equation of the second line is \(y=x+4\).
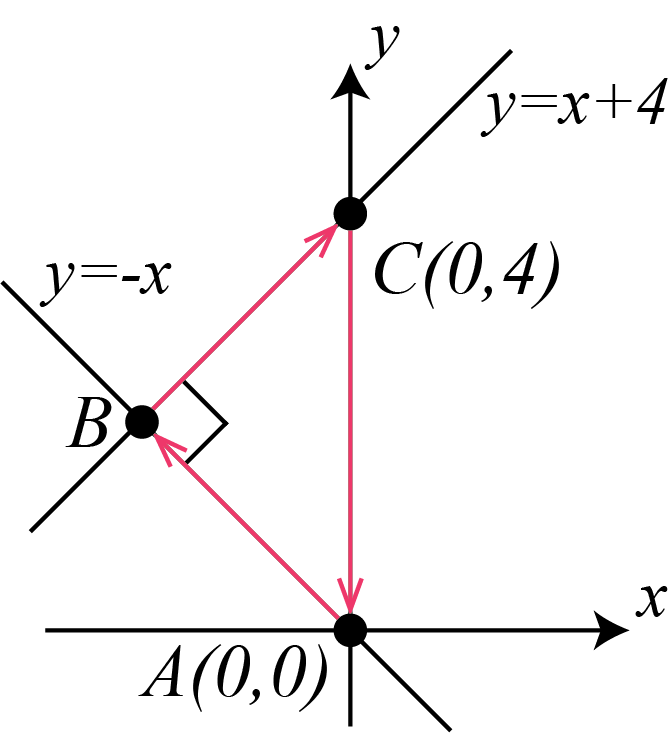
Since point \(B\) is located on both \(y=-x\) and \(y=x+4\), we can solve the system of equations to find the coordinates of \(B\). Since \(y=y\), \[\begin{aligned} -x&=x+4\\ -2x&=4\\ x&=-2\end{aligned}\] Substituting \(x=-2\) into \(y=-x\), we obtain \(y=2\). The coordinates of \(B\) are therefore \((-2,2)\).
Using the distance formula, we can find the lengths of \(AB\) and \(BC\). \[\begin{aligned} AB&=\sqrt{(-2-0)^2+(2-0)^2}=\sqrt{4+4}=\sqrt{8}\\ BC&=\sqrt{(0-(-2))^2+(4-2)^2}=\sqrt{4+4}=\sqrt{8}\end{aligned}\] The distance from point \(A\) to point \(C\) along the \(y\)-axis is \(AC=4\) km. That is, \(AC=4\).
Thus, the total distance walked by Hilde is \(AB+BC+AC=\sqrt{8}+\sqrt{8}+4=(2\sqrt{8}+4)\) km.
Note that the answer \(\left(2\sqrt{8}+4\right)\) is an exact answer. We can use a calculator to determine that this distance is approximately \(9.7\) km.
The exact total distance travelled can be further simplified as follows: \[2\sqrt{8}+4=2(\sqrt{4}\sqrt{2})+4=2(2\sqrt{2})+4=4\sqrt{2}+4\] This method of simplifying radicals is developed in later mathematics courses.
Solution 4
If you travel northwest from \(A (0,0)\), the line of travel will make a \(45^\circ\) angle with the positive \(y\)-axis. It follows that this line has slope \(-1\). Since this line passes through \(A(0,0)\) and has slope \(-1\), the equation of the line through \(A\) and \(B\) is \(y=-x\). A line drawn to the northeast would be perpendicular to a line drawn to the northwest, so \(AB\) is perpendicular to \(BC\), and thus \(\angle ABC=90^\circ\).
Point \(B\) is located somewhere on \(y=-x\). Let the coordinates of \(B\) be \((-b,b)\) for some \(b>0\).

Using the distance formula, we can find expressions for the lengths of \(AB\) and \(BC\). \[\begin{aligned} AB&=\sqrt{(-b-0)^2+(b-0)^2}=\sqrt{b^2+b^2}=\sqrt{2b^2}\\ BC&=\sqrt{(0-(-b))^2+(4-b)^2}=\sqrt{b^2+16-8b+b^2}=\sqrt{2b^2-8b+16}\end{aligned}\] The distance from point \(A\) to point \(C\) along the \(y\)-axis is \(AC=4\) km. That is, \(AC=4\).
Using the Pythagorean Theorem, we can find the value of \(b\). \[\begin{aligned} AC^2&=AB^2+BC^2\\ 4^2&=\left(\sqrt{2b^2}\right)^2+\left(\sqrt{2b^2-8b+16}\right)^2\\ 16&=2b^2+(2b^2-8b+16)\\ 16&=4b^2-8b+16\\ 0&=4b^2-8b\\ 0&=b^2-2b\\ 0&=b(b-2)\\ b&=0,2\end{aligned}\] Since \(b>0\), it follows that \(b=2\). We can substitute \(b=2\) into our expressions for \(AB\) and \(BC\). \[\begin{aligned} AB&=\sqrt{2b^2}=\sqrt{2(2)^2}=\sqrt{8}\\ BC&=\sqrt{2b^2-8b+16}=\sqrt{2(2)^2-8(2)+16}=\sqrt{8}\end{aligned}\]
Thus, the total distance walked by Hilde is \(AB+BC+AC=\sqrt{8}+\sqrt{8}+4=(2\sqrt{8}+4)\) km.
Note that the answer \(\left(2\sqrt{8}+4\right)\) is an exact answer. We can use a calculator to determine that this distance is approximately \(9.7\) km.
The exact total distance travelled can be further simplified as follows: \[2\sqrt{8}+4=2(\sqrt{4}\sqrt{2})+4=2(2\sqrt{2})+4=4\sqrt{2}+4\] This method of simplifying radicals is developed in later mathematics courses.