A Venn diagram has two circles, labelled A and B.
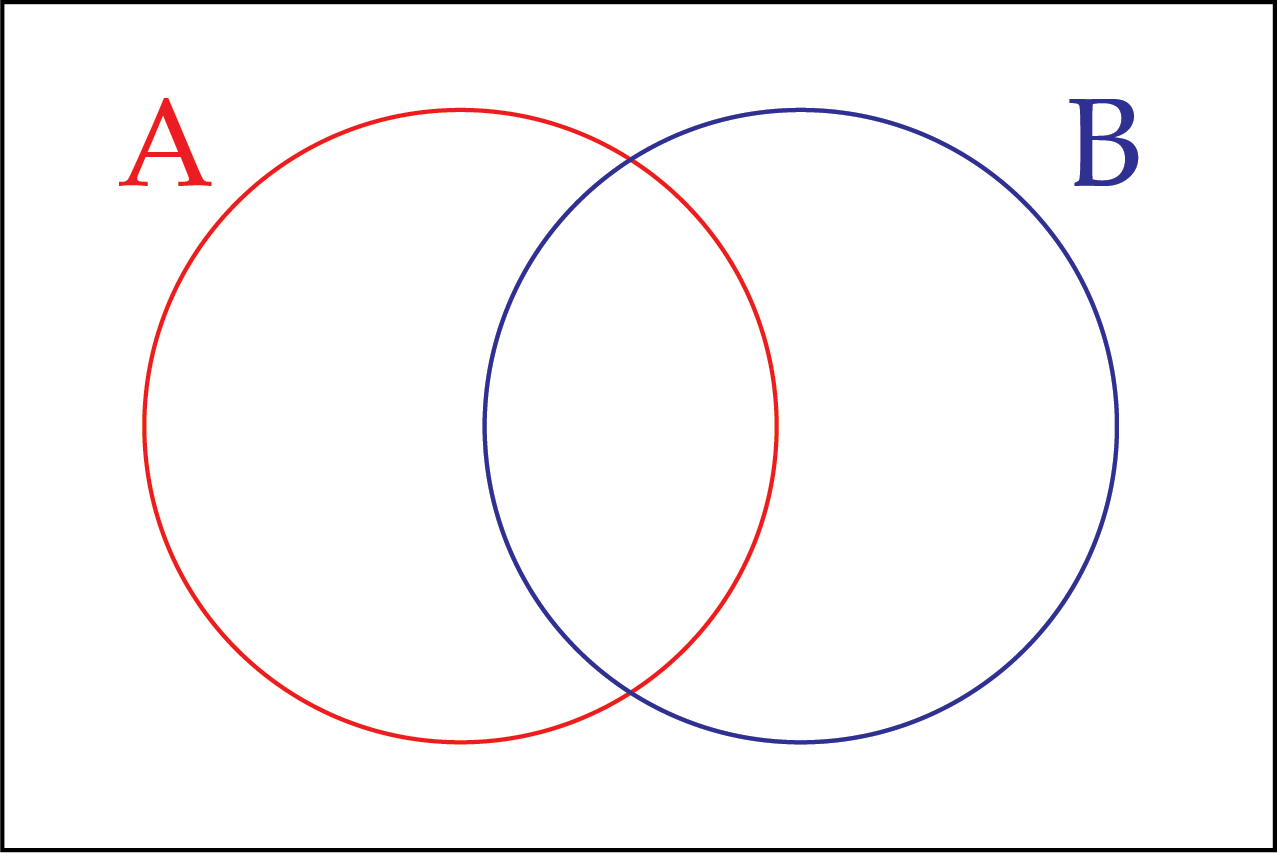
Each circle contains ordered pairs, \((x,y)\), where \(x\) and \(y\) are real numbers, that satisfy the following criteria.
A: \(y=-x+1\)
B: \(y=3x+5\)
The overlapping region in the middle contains ordered pairs that are in both A and B, and the region outside both circles contains ordered pairs that are neither in A nor B.
In total this Venn diagram has four regions. Place ordered pairs in as many of the regions as you can. Is it possible to find an ordered pair for each region?
A Venn diagram has three circles, labelled A, B, and C.
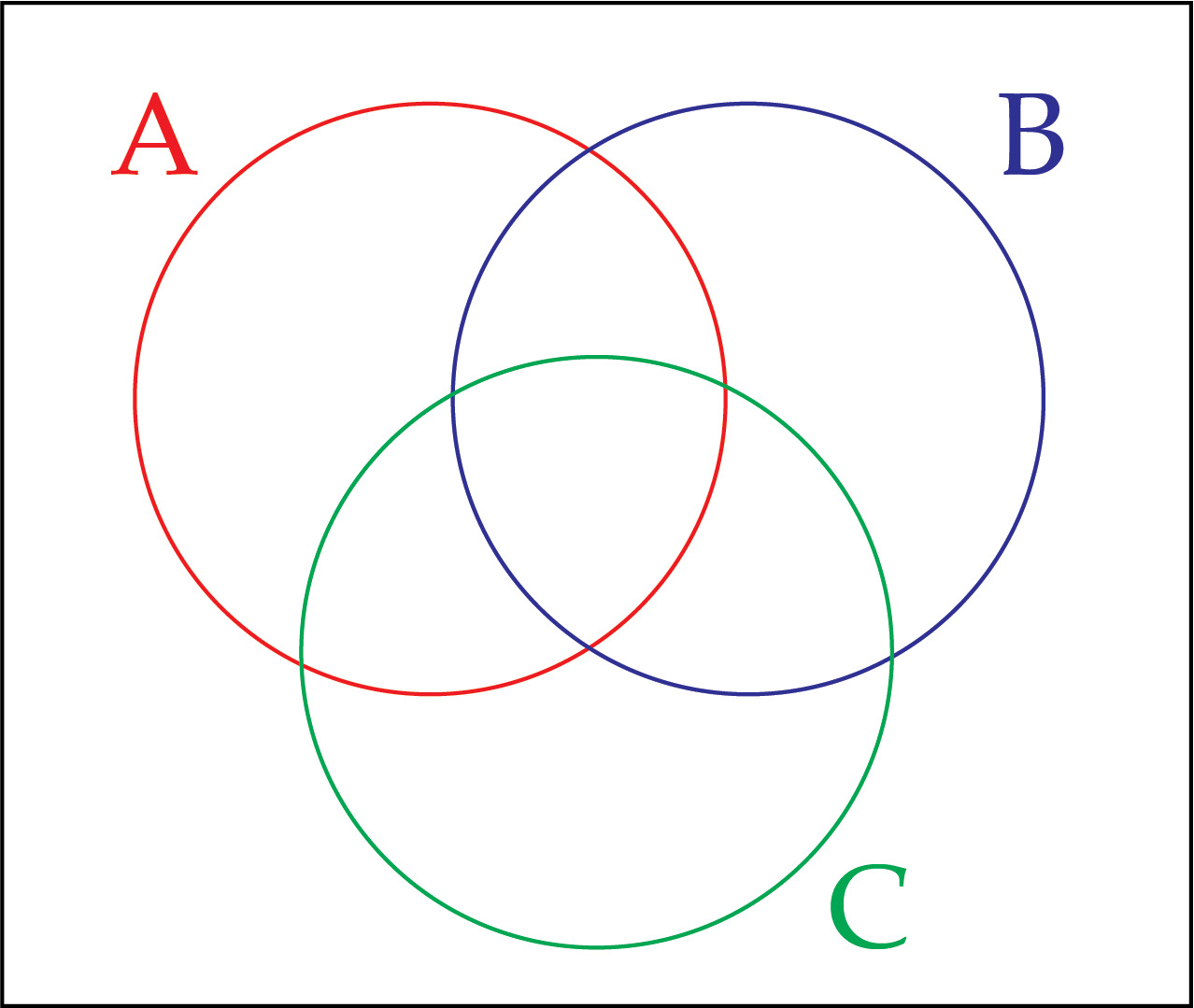
Each circle contains integers, \(n\), that satisfy the following criteria.
A: \(3n<20\)
B: \(n+9>6\)
C: \(n\) is even
In total this Venn diagram has eight regions. Place integers in as many of the regions as you can. Is it possible to find an integer for each region?
