
In \(\triangle ABC\), \(\angle ABC = 90^{\circ}\). A median is drawn from \(A\) to side \(BC\), meeting \(BC\) at \(M\) such that \(AM=5\). A second median is drawn from \(C\) to side \(AB\), meeting \(AB\) at \(N\) such that \(CN=2\sqrt{10}\).
Determine the length of the longest side of \(\triangle ABC\).

Note: In a triangle, a median is a line segment drawn from a vertex of the triangle to the midpoint of the opposite side.
Since \(AM\) is a median, \(M\) is the midpoint of \(BC\). Then \(BM=MC\). Let \(BM=MC=y\).
Since \(CN\) is a median, \(N\) is the midpoint of \(AB\). Then \(AN=NB\). Let \(AN=NB=x\).
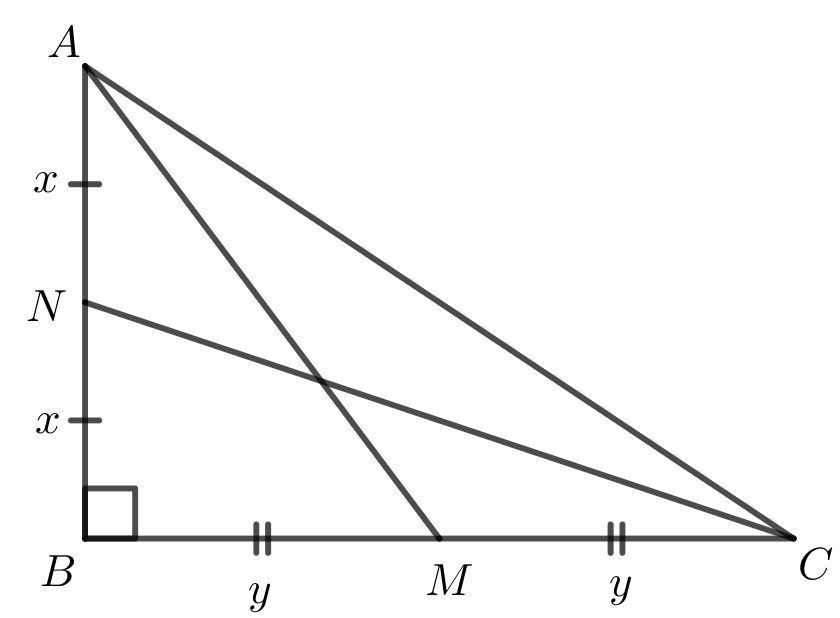
Since \(\angle B=90^{\circ}\), \(\triangle NBC\) is a right-angled triangle. Using the Pythagorean Theorem, \[\begin{align*} NB^2+BC^2&=CN^2\\ x^2+(2y)^2&=(2\sqrt{10})^2\\ x^2+4y^2&=40\tag{1}\end{align*}\]
Since \(\angle B=90^{\circ}\), \(\triangle ABM\) is a right-angled triangle. Using the Pythagorean Theorem, \[\begin{align*} AB^2+BM^2&=AM^2\\ (2x)^2+y^2&=5^2\\ 4x^2+y^2&=25 \tag{2}\end{align*}\]
Adding equations \((1)\) and \((2)\), we get \(5x^2+5y^2=65\) or \(x^2+y^2=13\).
The longest side of \(\triangle ABC\) is the hypotenuse \(AC\). Using the Pythagorean Theorem, \[\begin{aligned} AC^2&=AB^2+BC^2\\ &=(2x)^2+(2y)^2\\ &=4x^2+4y^2\\ &=4(x^2+y^2)\end{aligned}\]
Since \(x^2 + y^2 =13\), we have \(AC^2 = 4(13)\). And since \(AC>0\), \(AC=2\sqrt{13}\) follows.
Therefore, the length of the longest side of \(\triangle ABC\) is \(2\sqrt{13}\).
Note: The solver could have instead solved a system of equations to find \(x=2\) and \(y=3\), and then proceed to solve for the longest side. The above approach was provided to expose the solver to alternate way to think about the solution of this problem.