Case \(1\): \(t = 1\)
The two side faces that Jenny sees must sum to \(15 - 1 = 14\). Since the largest face value is \(6\), the maximum sum of the numbers on two faces is \(5+6= 11\). Therefore, it is not possible for the numbers on two side faces to sum to \(14\), and so the number on the top face cannot be \(1\).
Case \(2\): \(t = 2\)
The two side faces that Jenny sees must sum to \(15 - 2 = 13\). Again, the maximum sum of the numbers on two faces is \(5+6= 11\). Therefore, it is not possible for the numbers on two side faces to sum to \(13\), and so the number on the top face cannot be \(2\).
Case \(3\): \(t = 3\)
The two side faces that Jenny sees must sum to \(15 - 3 = 12\). Again, the maximum sum of the numbers on two faces is \(5+6= 11\). Therefore, it is not possible for the numbers on two side faces to sum to \(12\), and so the number on the top face cannot be \(3\).
Case \(4\): \(t = 4\)
The two side faces that Jenny sees must sum to \(15 - 4 = 11\). It is possible to get a sum of \(11\), and the only possible way is with the numbers on the two faces being \(5\) and \(6\).
Now, the two side faces that Lee sees must sum to \(14 - 4 = 10\). The only possible way to get a sum of \(10\) is with the numbers on the two faces being \(4\) and \(6\). But the number on the top face is also \(4\), so it is not possible to have a \(4\) on a side face.
Therefore, the number on the top face cannot be \(4\).
Case \(5\): \(t = 5\)
The two side faces that Jenny sees must sum to \(15 - 5 = 10\). The only possible way to get a sum of \(10\) is with the two faces being \(4\) and \(6\).
Now, the two side faces that Lee sees must sum to \(14 - 5 = 9\). It is possible to get a sum of \(9\), and the only possible ways are with the numbers on the two faces being \(4\) and \(5\) or \(3\) and \(6\). Since the number on the top face is \(5\), then the numbers on the two side faces cannot be \(4\) and \(5\). Therefore, the numbers on two side faces that Lee sees must be \(3\) and \(6\).
Finally, the two side faces that Paul sees must sum to \(9 - 5 = 4\). It is possible to get a sum of \(4\), and the only possible way is with the numbers on the faces being \(1\) and \(3\).
Therefore, it is possible for the number on the top face to be \(5\). Then the numbers on the four side faces must be \(4\), \(6\), \(3\), and \(1\). Each person’s view is shown below.
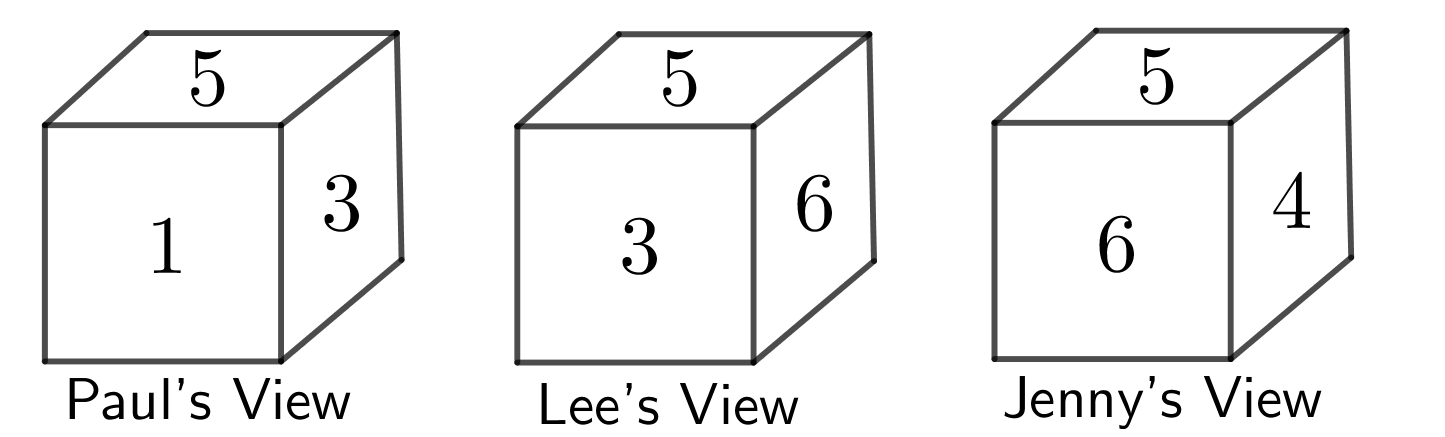
The visible numbers are \(1\), \(3\), \(4\), \(5\), and \(6\). Therefore, the number on the bottom of the cube is \(2\).
Case \(6\): \(t = 6\)
The two side faces that Jenny sees must sum to \(15 - 6 = 9\). It is possible to get a sum of \(9\), and the only possible ways are with the numbers on the two faces being \(3\) and \(6\), or \(4\) and \(5\). Since the number on the top face is \(6\), then the numbers on the two side faces cannot be \(3\) and \(6\). Therefore, the numbers on the two side faces that Jenny sees must be \(4\) and \(5\).
Now, the two side faces that Lee sees must sum to \(14 - 6 = 8\). It is possible to get a sum of \(8\), and the only possible ways are with the numbers on the two faces being \(2\) and \(6\) or \(3\) and \(5\). Since the number on the top face is \(6\), then the numbers on the two side faces cannot be \(2\) and \(6\). Therefore, the numbers on the two side faces that Lee sees must be \(3\) and \(5\).
Finally, the two side faces that Paul sees must sum to \(9 - 6 = 3\). The only possible way to get a sum of \(3\) is with the faces being \(1\) and \(2\).
From Jenny’s, Lee’s and Paul’s views, we know that the side faces must have numbers \(4\), \(5\), \(3\), \(1\), and \(2\). But there are only four side faces, so it is impossible for each of these five numbers to appear on a side face.
Therefore, it is not possible for the number on the top face of the cube to be \(6\).
