




































Sabrina is playing a video game that uses a \(6\) by \(6\) grid. Her character starts in the top-left square and needs to get to the house in the bottom-right corner. All the other squares contain either fish or penguins, as shown in the following grid.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Sabrina can move only right or down through the grid. When she gets to a square with fish, she picks up all the fish. When she gets to a square with penguins, she must feed one fish to each penguin.
If Sabrina starts with \(5\) fish, what is the maximum possible number of fish she could have with her when she arrives at the house?
This problem was inspired by a past Beaver Computing Challenge (BCC) problem.
One way to solve this problem is by counting the number of fish Sabrina has as she moves through the grid, recording the maximum possible number of fish for each square. To start, Sabrina has \(5\) fish. If she moves to the right then she lands on a square with one penguin. After feeding it she has \(5-1=4\) fish. If she instead moves down initially, then she lands on a square with one fish. After picking it up, she has \(5+1=6\) fish. There are two ways to get to the square in the second row and second column. If Sabrina comes from the left, she will have \(6\) fish, but if she comes from above, she will have only \(4\) fish. Since \(6>4\), the best way to reach the square in the second row and second column is to come from the left. We record this on our grid with an arrow. Then, since the square in the second row and second column has one fish, Sabrina will pick it up and then have \(6+1=7\) fish.

In this way, for each square we calculate the total possible number of fish coming from the left or from above, and use the higher number in that square. Each arrow indicates the direction from which the higher number was calculated. The completed grid is shown. A shaded path through the squares in the grid is also indicated. Following the shaded path allows Sabrina to end up with the maximum possible number of fish when she arrives at the house.
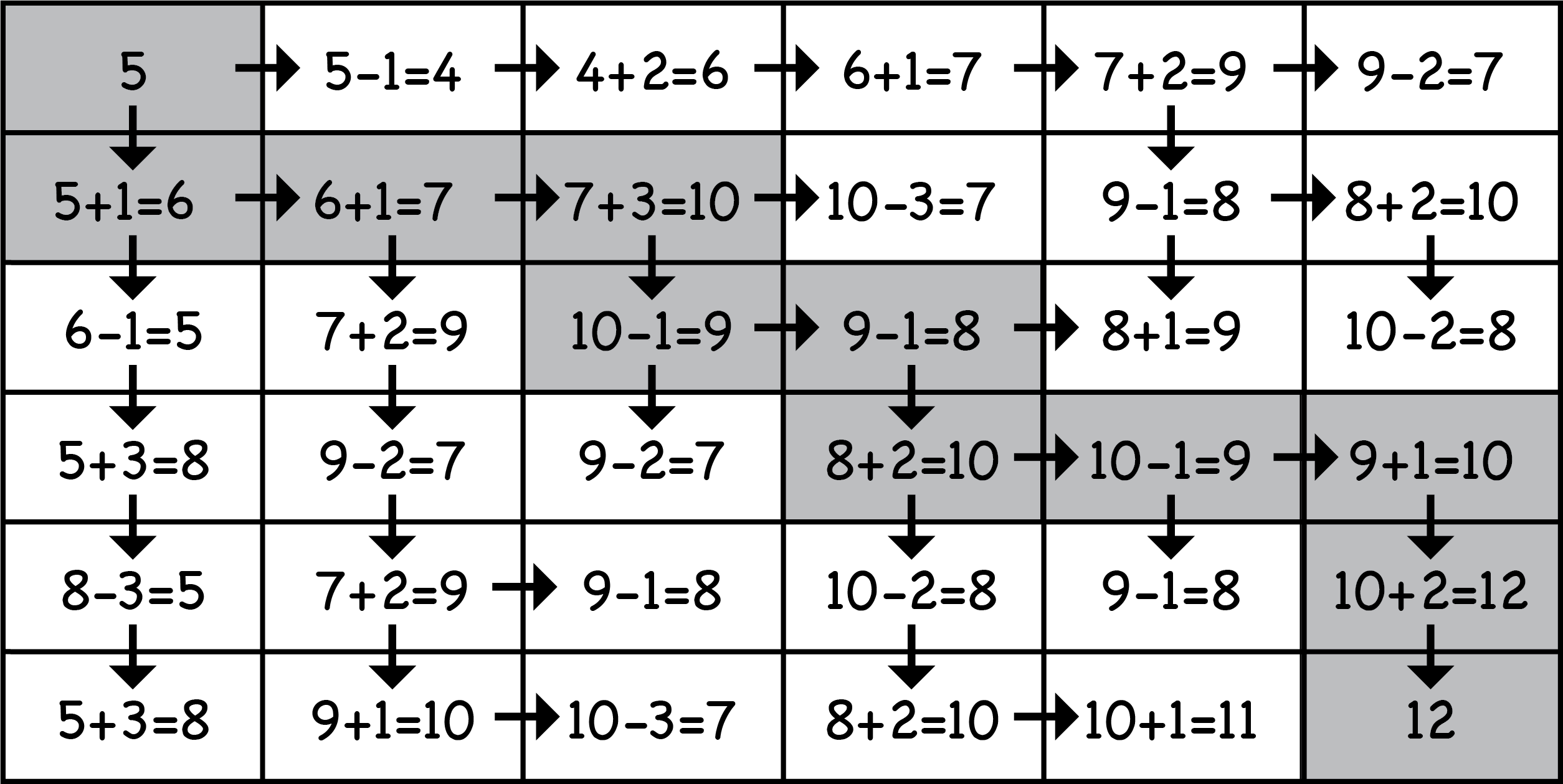
Thus, the maximum possible number of fish Sabrina could have with her when she arrives at the house is \(12\).