Problem of the Week
Problem E and Solution
Everything in its Place 3

Problem

1. A Venn diagram has two circles, labelled A and B.

   

   Each circle contains functions, \(f(x)\), that satisfy the following criteria.

   • A: \(f(2)=-3\)

   • B: \(f(-2)=-1\)

   The overlapping region in the middle contains functions that are in both A and B, and the region outside both circles contains functions that are neither in A nor B.

   In total this Venn diagram has four regions. Place functions in as many of the regions as you can. Is it possible to find a function for each region?

2. A Venn diagram has three circles, labelled A, B, and C.

   

   Each circle contains ordered pairs, \((x,y)\), where \(x\) and \(y\) are real numbers, that satisfy the following criteria.

   • A: \(y=(x+3)^3+2\)

   • B: \(y=\dfrac{1}{2}x^2+1\)

   • C: \(y=|x+1|\)

   In total this Venn diagram has eight regions. Place ordered pairs in as many of the regions as you can. Is it possible to find an ordered pair for each region?

Solution

1. We have marked the four regions W, X, Y, and Z.

   

   When creating functions, you can think of the problem algebraically, or graphically. When thinking algebraically, a function that satisfies \(f(2)=-3\) is one that evaluates to \(-3\) when \(2\) is substituted for \(x\). When thinking graphically, a function that satisfies \(f(2)=-3\) is one whose graph goes through the point \((2,-3)\).

   • Any function in region W must satisfy \(f(2)=-3\) but not \(f(-2)=-1\). There are infinitely many possibilities. Some examples are \(f(x)=-x-1\) and \(f(x)=x^2-7\).

   • Any function in region X must satisfy both \(f(2)=-3\) and \(f(-2)=-1\). In other words, the graph of the function must pass through both \((2,-3)\) and \((-2,-1)\). There are infinitely many possibilities. Some examples are \(f(x)=-\frac{1}{2}x-2\) and \(f(x)=-\frac{1}{8}x^3-2\).

   • Any function in region Y must satisfy \(f(-2)=-1\) but not \(f(2)=-3\). There are infinitely many possibilities. Some examples are \(f(x)=\frac{1}{2}x\) and \(f(x)=x^2-5\).

   • Any function in region Z must satisfy neither \(f(2)=-3\) nor \(f(-2)=-1\). There are again infinitely many possibilities. Some examples are \(f(x)=x\) and \(f(x)=x^2\).

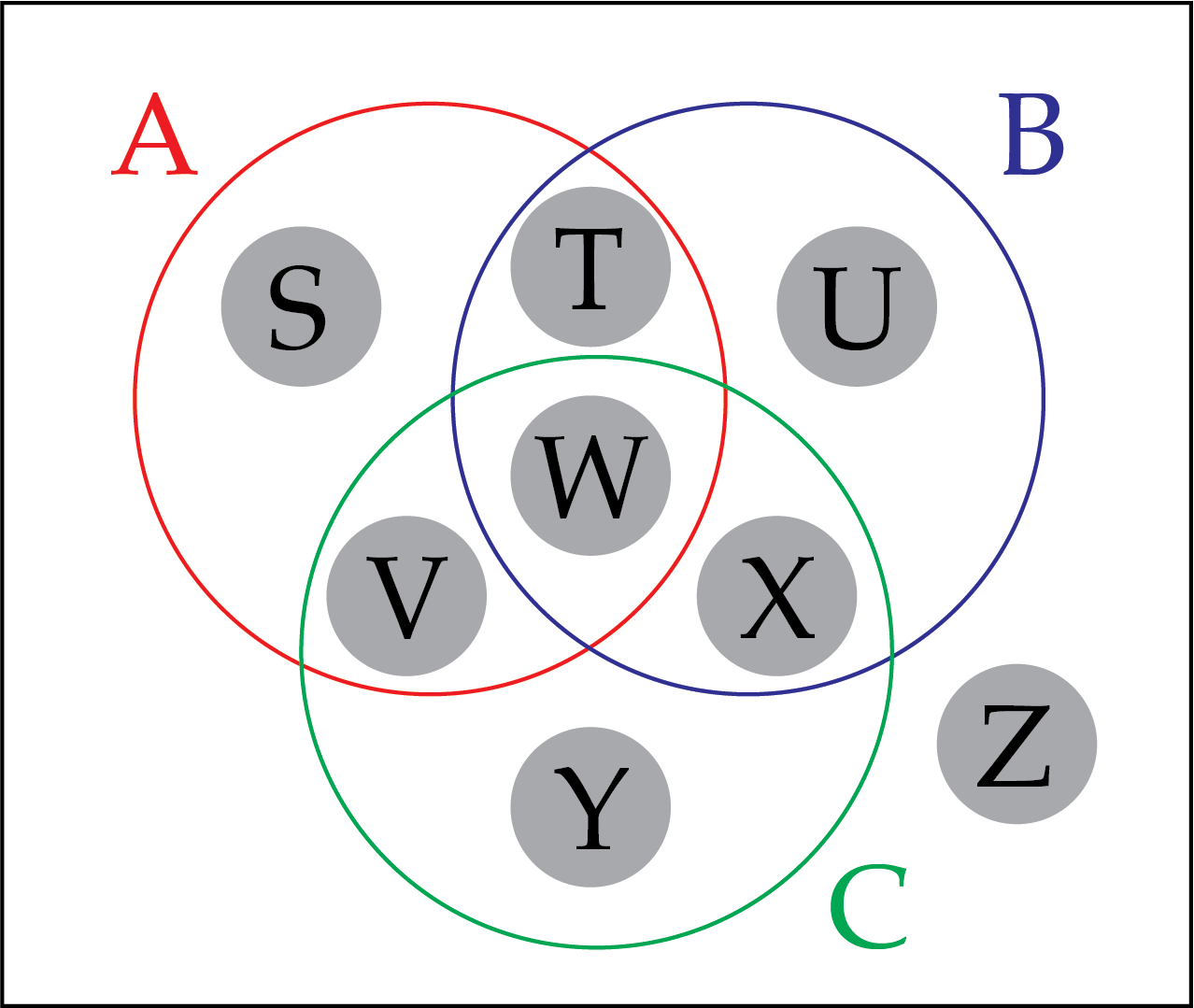
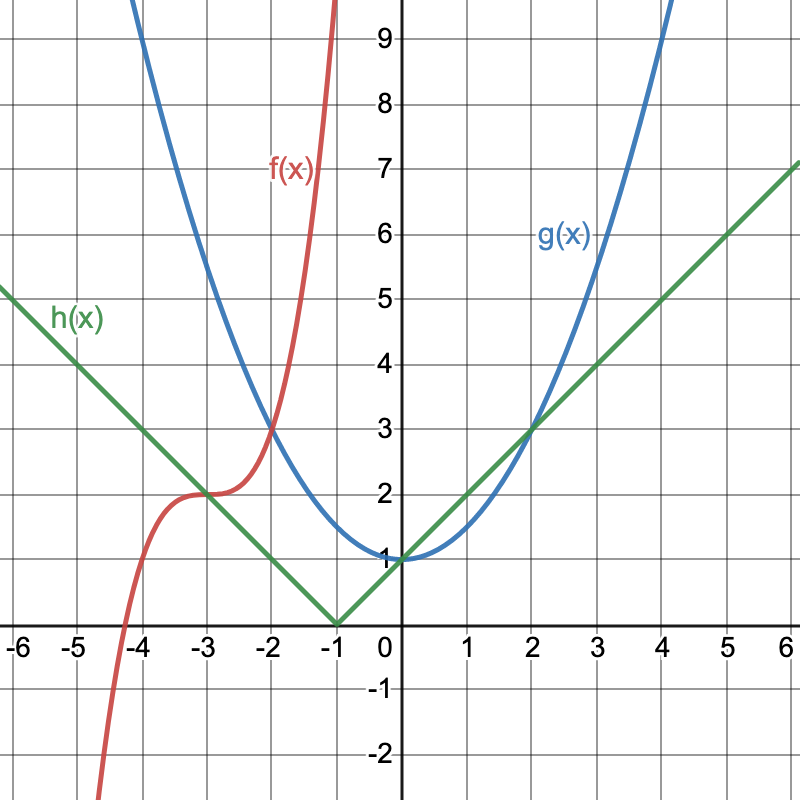
2. We have marked the eight regions S, T, U, V, W, X, Y, and Z.

   

   Hide/Reveal Description of the Regions

   1. Region S is the region lying inside circle A, outside circle B, and outside circle C.

   2. Region T is inside A, inside B, and outside C.

   3. Region U is inside B, outside A, and outside C.

   4. Region V is inside A, inside C, and outside B.

   5. Region W is inside all three circles.

   6. Region X is inside B, inside C, and outside A.

   7. Region Y inside C, outside A, and outside B.

   8. Region Z is outside all three circles.

   ---

   We will name the functions as follows: \(f(x)=(x+3)^3+2\), \(g(x)=\frac{1}{2}x^2+1\), and \(h(x)=|x+1|\). We have also provided a graph of the functions.

   

   Note that the graphs of \(f\) and \(g\) intersect at \((-2,3)\), the graphs of \(f\) and \(h\) intersect at \((-3,2)\), and the graphs of \(g\) and \(h\) intersect at \((0,1)\) and \((2,3)\).

   • Any ordered pair in region S must satisfy the equation \(y=f(x)\), but not \(y=g(x)\) or \(y=h(x)\). Since the point \((-4,1)\) is on the graph of \(f\), but not on the graph of \(g\) or \(h\), the ordered pair \((-4,1)\) works. There are infinitely many others as well.

   • Any ordered pair in region T must satisfy the equations \(y=f(x)\) and \(y=g(x)\), but not \(y=h(x)\). Since the point \((-2,3)\) is on the graph of \(f\) and on the graph of \(g\), but not on the graph of \(h\), the ordered pair \((-2,3)\) works. In fact, since \((-2,3)\) is the only point of intersection of the graphs of \(f\) and \(g\), this is the only possible choice for region T.

   • Any ordered pair in region U must satisfy the equation \(y=g(x)\), but not \(y=f(x)\) or \(y=h(x)\). The ordered pair \((4,9)\) works. There are infinitely many others as well.

   • Any ordered pair in region V must satisfy the equations \(y=f(x)\) and \(y=h(x)\), but not \(y=g(x)\). The ordered pair \((-3,2)\) works. In fact, since \((-3,2)\) is the only point of intersection of the graphs of \(f\) and \(h\), this is the only possible choice for region V.

   • Any ordered pair in region W must satisfy the equations \(y=f(x)\), \(y=g(x)\), and \(y=h(x)\). There are no ordered pairs that satisfy this as the graphs of the three functions do not have a common point of intersection. So this region must remain empty.

   • Any ordered pair in region X must satisfy the equations \(y=g(x)\) and \(y=h(x)\), but not \(y=f(x)\). The ordered pairs \((0,1)\) and \((2,3)\) work. In fact, since these are the only points of intersection of the graphs of \(g\) and \(h\), these are the only possible choices for region X.

   • Any ordered pair in region Y must satisfy the equation \(y=h(x)\), but not \(y=f(x)\) or \(y=g(x)\). The ordered pair \((-2,1)\) works. There are infinitely many others as well.

   • Any ordered pair in region Z must not satisfy the equations \(y=f(x)\), \(y=g(x)\), or \(y=h(x)\). The ordered pair \((0,0)\) works. There are infinitely many others as well.