

A rectangular piece of paper, \(PQRS\), has \(PQ = 30\) cm and \(PS = 40\) cm. The paper has grey lines on one side and is plain white on the other.

The paper is folded so that the two diagonally opposite corners \(P\) and \(R\) coincide. This creates a crease along line segment \(AC\), with \(A\) on \(PS\) and \(C\) on \(QR\).

Determine the length of \(AC\).
Since \(PQRS\) is a rectangle, all angles inside \(PQRS\) are \(90^\circ\). After the fold, \(R\) coincides with \(P\). Label the point that \(S\) folds to as \(D\). The angle at \(D\) is the same as the angle at \(S\). Since \(PQRS\) is a rectangle, \(\angle PSR=90^\circ\) and \(SR = 30\), and it follows that \(\angle PDA=90^\circ\) and \(PD = 30\).
Let \(a\) represent the length of \(QC\) and \(b\) represent the length of \(AS\).
Then \(CR=QR - QC=40-a\) and \(PA=PS-AS=40-b\).
Since \(S\) folds to \(D\), it follows that \(AD=AS=b\).
Since \(R\) folds to \(P\), it follows that \(PC=CR=40-a\).
All of the information is recorded on the following diagram.
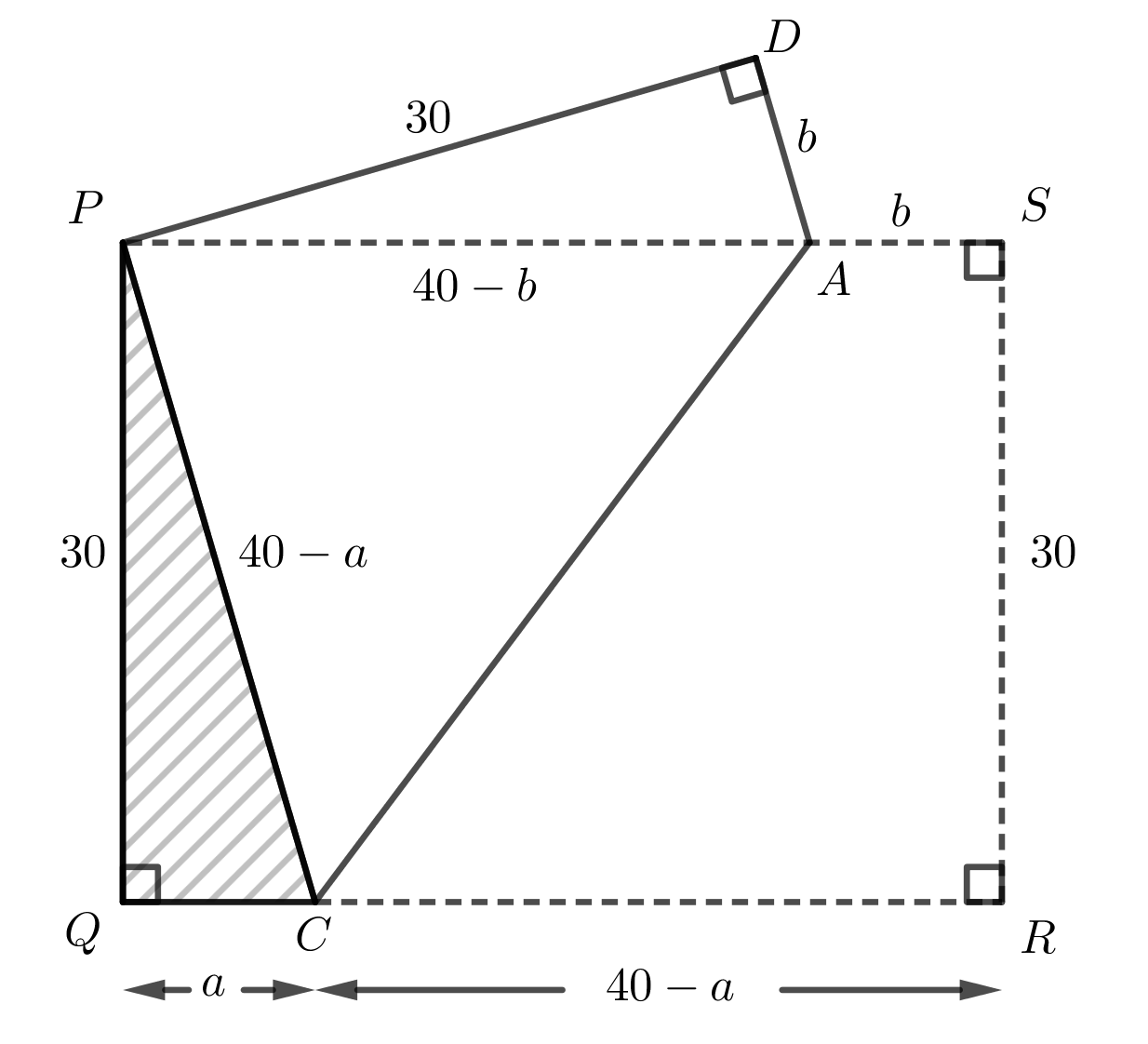
Since \(\triangle PQC\) is a right-angled triangle, we can use the Pythagorean Theorem to find \(a\). \[\begin{aligned} QC^2+PQ^2&=PC^2\\ a^2+30^2&=(40-a)^2\\ a^2+900&=1600-80a+a^2\\ 80a&=700\\ a&=\dfrac{35}{4}\end{aligned}\]
Since \(\triangle PDA\) is a right-angled triangle, we can use the Pythagorean Theorem to find \(b\). \[\begin{aligned} AD^2+PD^2&=PA^2\\ b^2+30^2&=(40-b)^2\\ b^2+900&=1600-80b+b^2\\ 80b&=700\\ b&=\dfrac{35}{4}\end{aligned}\]
Therefore, \(a=b=\dfrac{35}{4}\) cm.
We still need to find the length of the crease. From \(A\) drop a perpendicular to \(QR\) intersecting \(QR\) at \(B\). Then \(ABRS\) is a rectangle. It follows that \(AB=SR=30\) and \(BR=AS=b\).
Also, \(CB=QR-QC-BR=40-a-b=40-\dfrac{35}{4}-\dfrac{35}{4}=\dfrac{90}{4}=\dfrac{45}{2}\) cm.
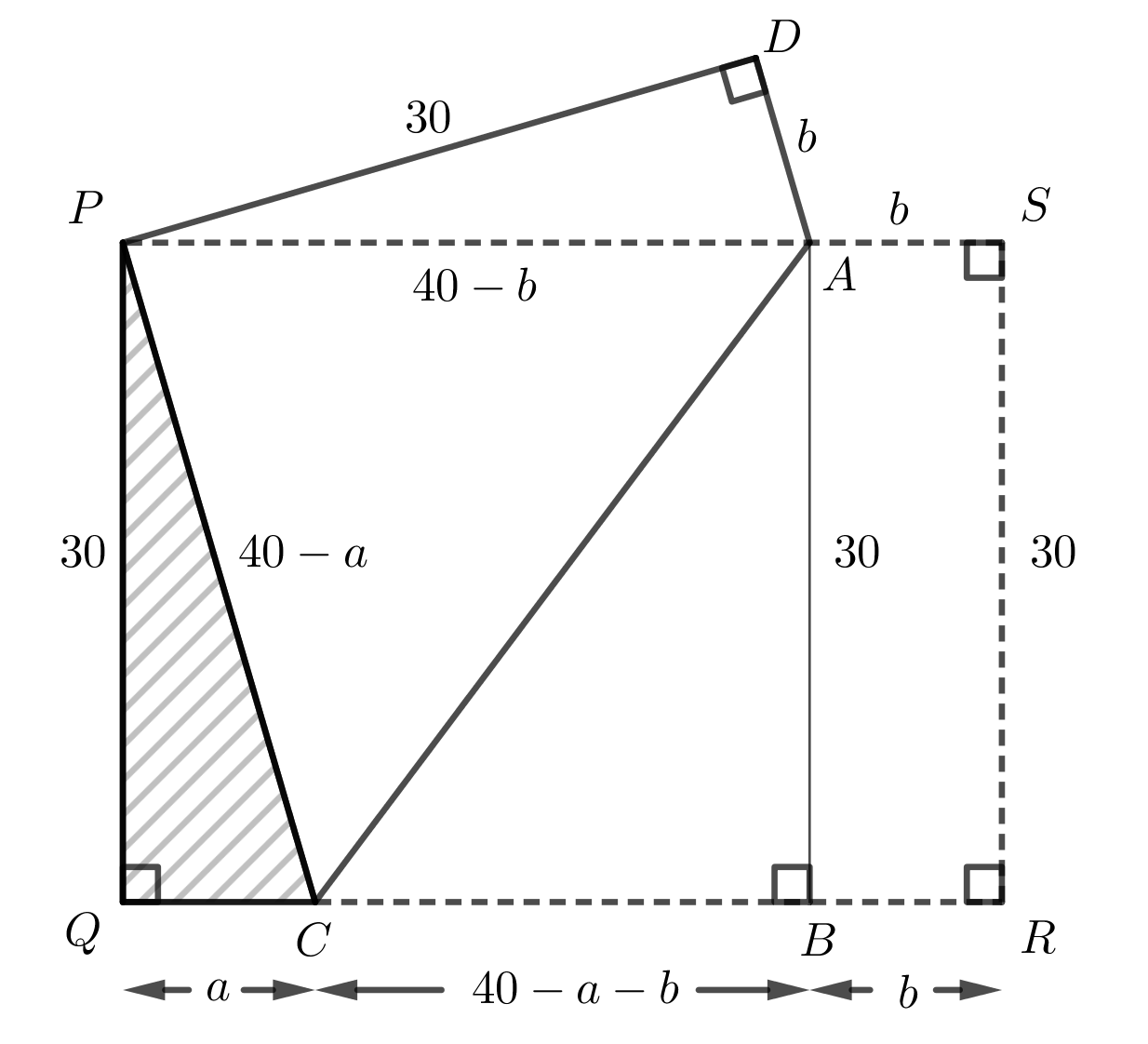
Using the Pythagorean Theorem in \(\triangle CAB\), \[\begin{aligned} AC^2&=AB^2+CB^2\\ &=30^2+\left(\dfrac{45}{2}\right)^2\\ &=900+\dfrac{2025}{4}\\ &=\dfrac{5625}{4}\end{aligned}\] Since \(AC >0\), it follows that \(AC=\dfrac{75}{2} = 37.5\) cm. Therefore, the length of the crease is \(\dfrac{75}{2}\) cm.