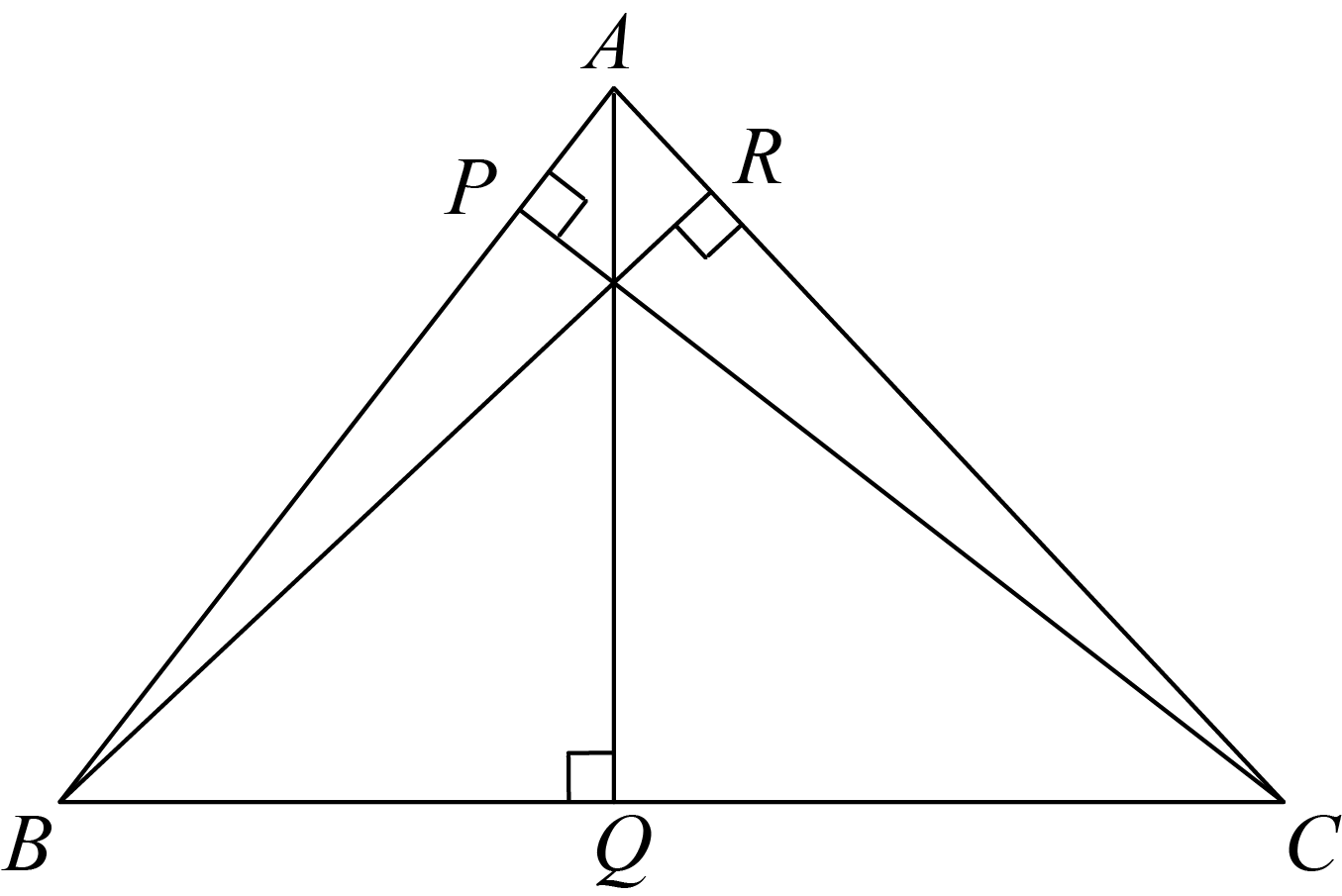

In triangle \(ABC\), point \(P\) lies on \(AB\), point \(Q\) lies on \(BC\), and point \(R\) lies on \(AC\) such that \(AQ\), \(BR\), and \(CP\) are altitudes with lengths \(21\) cm, \(24\) cm, and \(56\) cm, respectively.

Determine the measure, in degrees, of \(\angle ABC\), and the lengths, in centimetres, of \(AB\), \(BC\), and \(CA\).
Note the diagram is not drawn to scale.