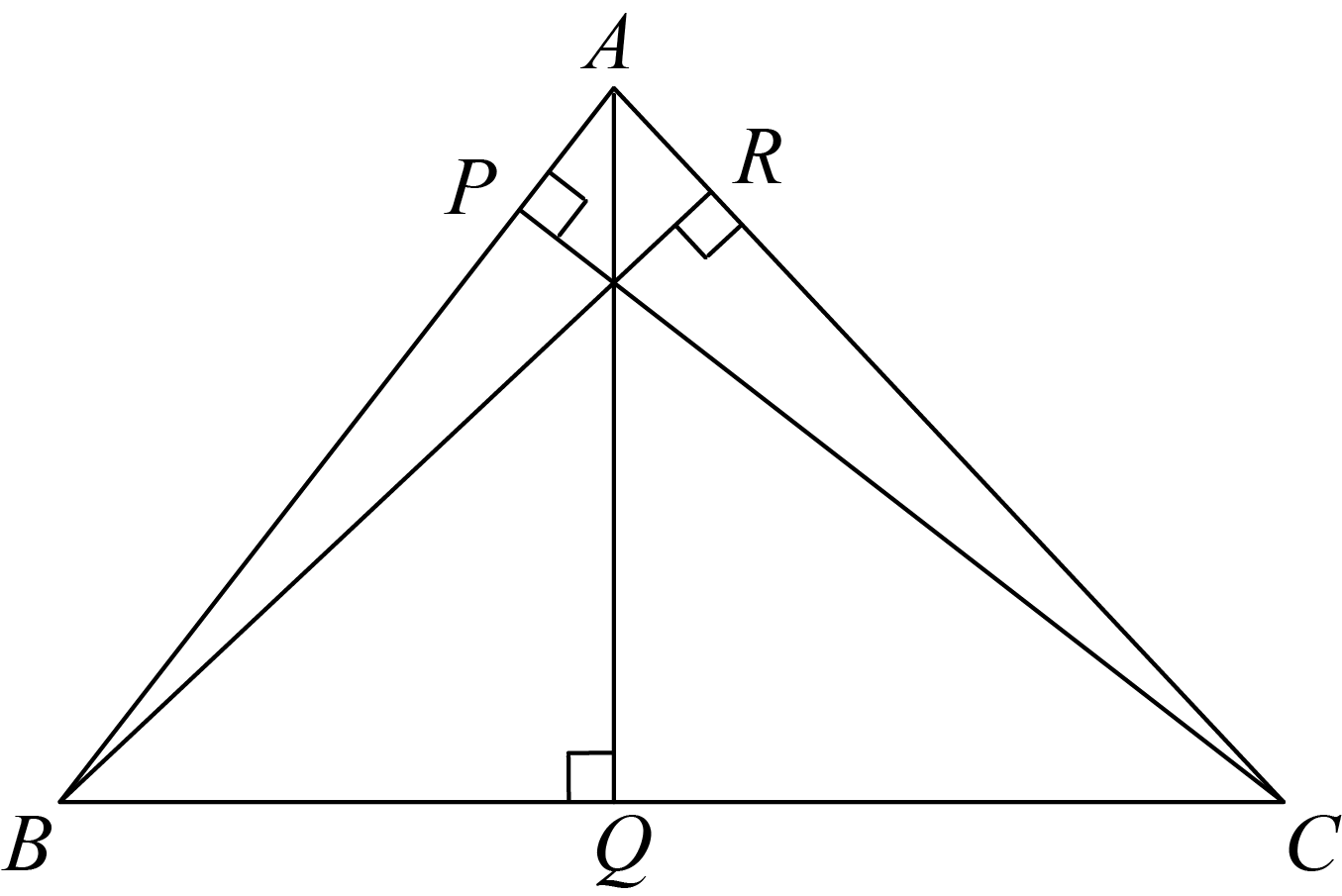

In triangle \(ABC\), point \(P\) lies on \(AB\), point \(Q\) lies on \(BC\), and point \(R\) lies on \(AC\) such that \(AQ\), \(BR\), and \(CP\) are altitudes with lengths \(21\) cm, \(24\) cm, and \(56\) cm, respectively.

Determine the measure, in degrees, of \(\angle ABC\), and the lengths, in centimetres, of \(AB\), \(BC\), and \(CA\).
Note the diagram is not drawn to scale.
Let \(BC=a\), \(AC=b\), and \(AB=c\). We will present two methods for determining that \(21a=24b=56c\), and then continue on with the rest of the solution.
Method 1: Use Areas
We can find the area of \(\triangle ABC\) by multiplying the length of the altitude (the height) by the corresponding base and dividing by 2. Therefore, \[\frac{AQ\times BC}{2}=\frac{BR\times AC}{2}=\frac{CP\times AB}{2}\] Substituting \(AQ=21\), \(BR=24\), and \(CP=56\), and multiplying through by \(2\) gives us \(21a=24b=56c\).
Method 2: Use Trigonometry
In right-angled \(\triangle ARB\), \(\sin A=\frac{BR}{AB}=\frac{24}{c}\). In \(\triangle APC\), \(\sin A=\frac{CP}{AC}=\frac{56}{b}\). Putting these together gives \(\frac{24}{c}=\frac{56}{b}\), or \(24b=56c\).
In right-angled \(\triangle BAQ\), \(\sin B=\frac{AQ}{AB}=\frac{21}{c}\). In \(\triangle BPC\), \(\sin B=\frac{CP}{BC}=\frac{56}{a}\). Putting these together gives \(\frac{21}{c}=\frac{56}{a}\), or \(21a=56c\).
Combining these gives \(21a=24b=56c\).
We now will continue on with the rest of the solution.
From \(21a=24b\) we obtain \(b=\frac{21}{24}a=\frac{7}{8}a\), and from \(21a=56c\) we obtain \(c=\frac{21}{56}a=\frac{3}{8}a\).
The ratio of the sides in \(\triangle ABC\) is therefore \(a:b:c=a:\frac{7}{8}a:\frac{3}{8}a=8:7:3\). Let \(BC=8x\), \(AC=7x\), and \(AB=3x\), where \(x>0\).
Using the cosine law, \[\begin{aligned} AC^2&=AB^2+BC^2-2(AB)(BC)\cos(\angle ABC)\\ (7x)^2&=(3x)^2+(8x)^2-2(3x)(8x)\cos(\angle ABC)\\ 49x^2&=9x^2+64x^2-48x^2\cos(\angle ABC)\end{aligned}\] Since \(x>0\), we know \(x^2\neq 0\). So dividing by \(x^2\), \[49=73-48\cos(\angle ABC)\] Rearranging, \[\begin{aligned} 48\cos(\angle ABC)&=24\\ \cos(\angle ABC)&=\frac{1}{2}\end{aligned}\] Therefore, \(\angle ABC=60^\circ\).
In right \(\triangle BPC\), \[\begin{aligned} \frac{CP}{BC}&=\sin 60^\circ\\ BC&=\frac{CP}{\sin 60^\circ}\\ BC&=\frac{56}{\frac{\sqrt{3}}{2}}\\ BC&=\frac{112}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}\\ BC&=\frac{112\sqrt{3}}{3}\end{aligned}\] However, \(BC=8x\). Therefore, \[\begin{aligned} 8x&=\frac{112\sqrt{3}}{3}\\ x&=\frac{14\sqrt{3}}{3}\\ 3x&=14\sqrt{3}\\ 7x&=\frac{98\sqrt{3}}{3}\end{aligned}\]
Therefore, \(\angle ABC=60^\circ\), and the side lengths of \(\triangle ABC\) are \(AB=3x=14\sqrt{3}\) cm, \(AC=7x=\dfrac{98\sqrt{3}}{3}\) cm, and \(BC=\dfrac{112\sqrt{3}}{3}\) cm.